Welcome to the International version of the Statistical Extrapolation Bayesian Analyzer Projection System, which is, of course, a tortured gathering of words used to create the SEBA Projection System (which is emitting a sad, Colorado odor at the moment).
The system consists of a model projecting the probabilities of game results and then a barrage of simulations which account for the remaining luck. So the probabilities you see below show, essentially, what the odds are of an outcome if the team continues to play like it has been.
Below are the current Women’s Olympic tournament forecasts through August 3.
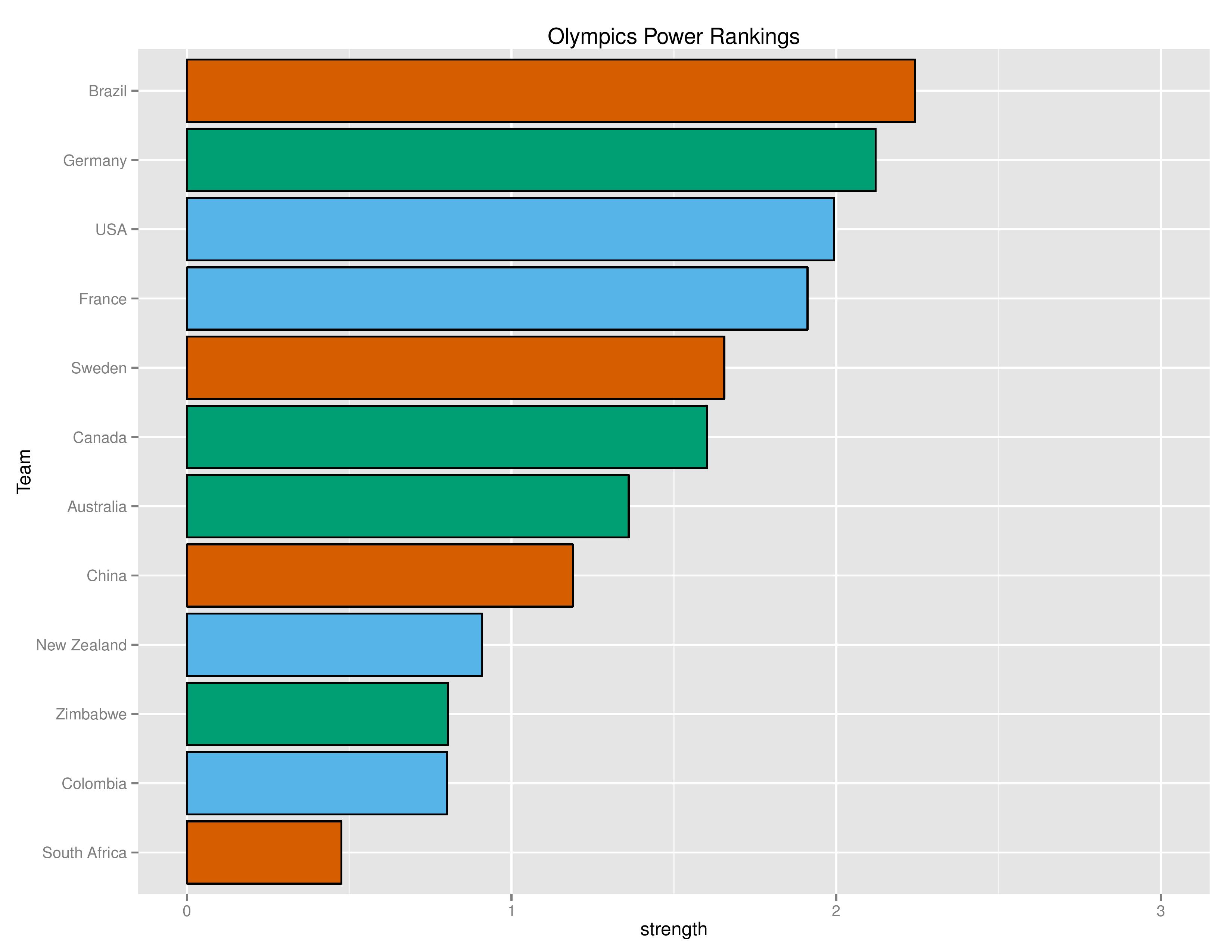
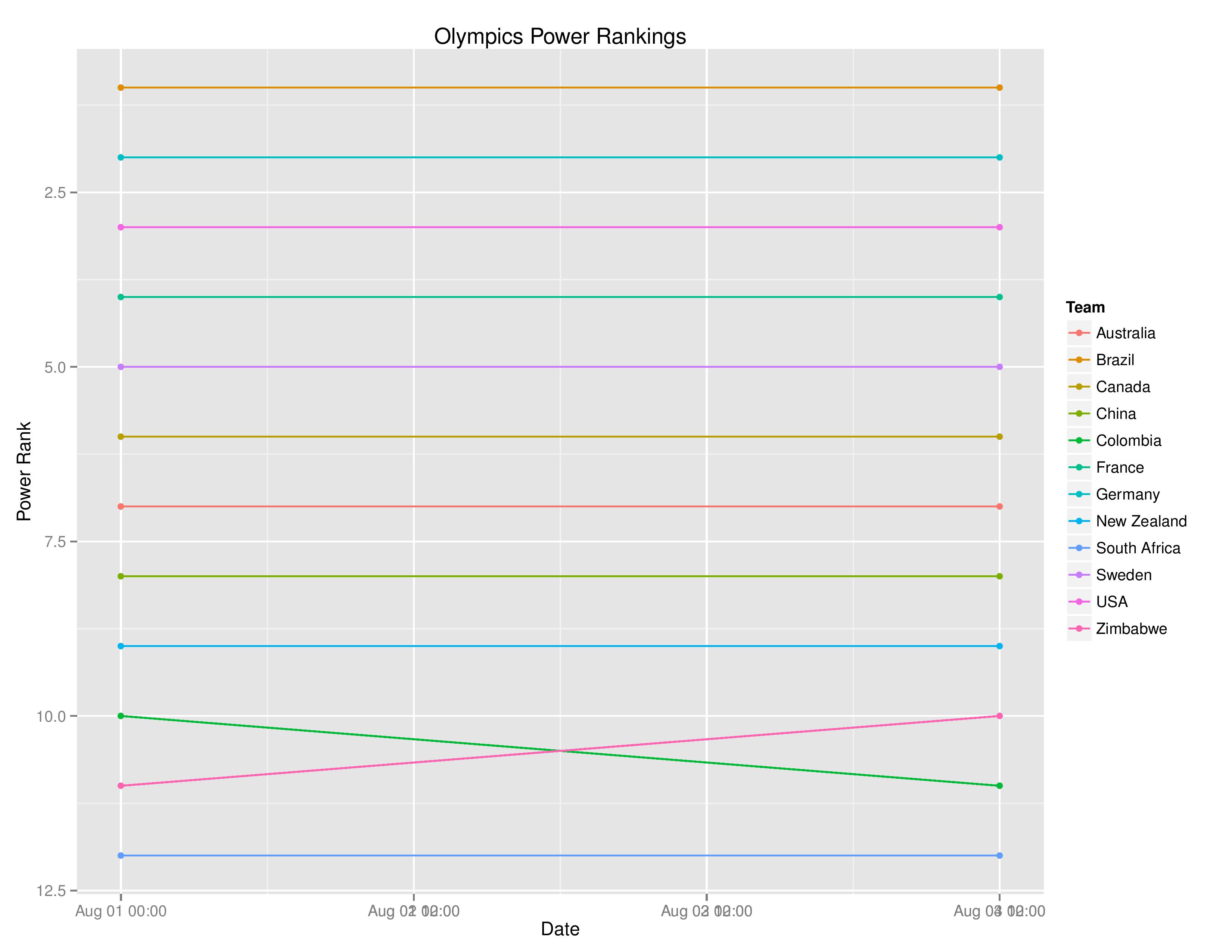
Power Rankings
The “Power Rankings” we concoct are the actual “strength” of the team according to competitive expectations. The value represented on the X-Axis is the average amount of points we expect that team to receive if they played every other team in the tournament.
The colors represent the groups.
Keep in mind that Brazil’s home field advantage is included below:
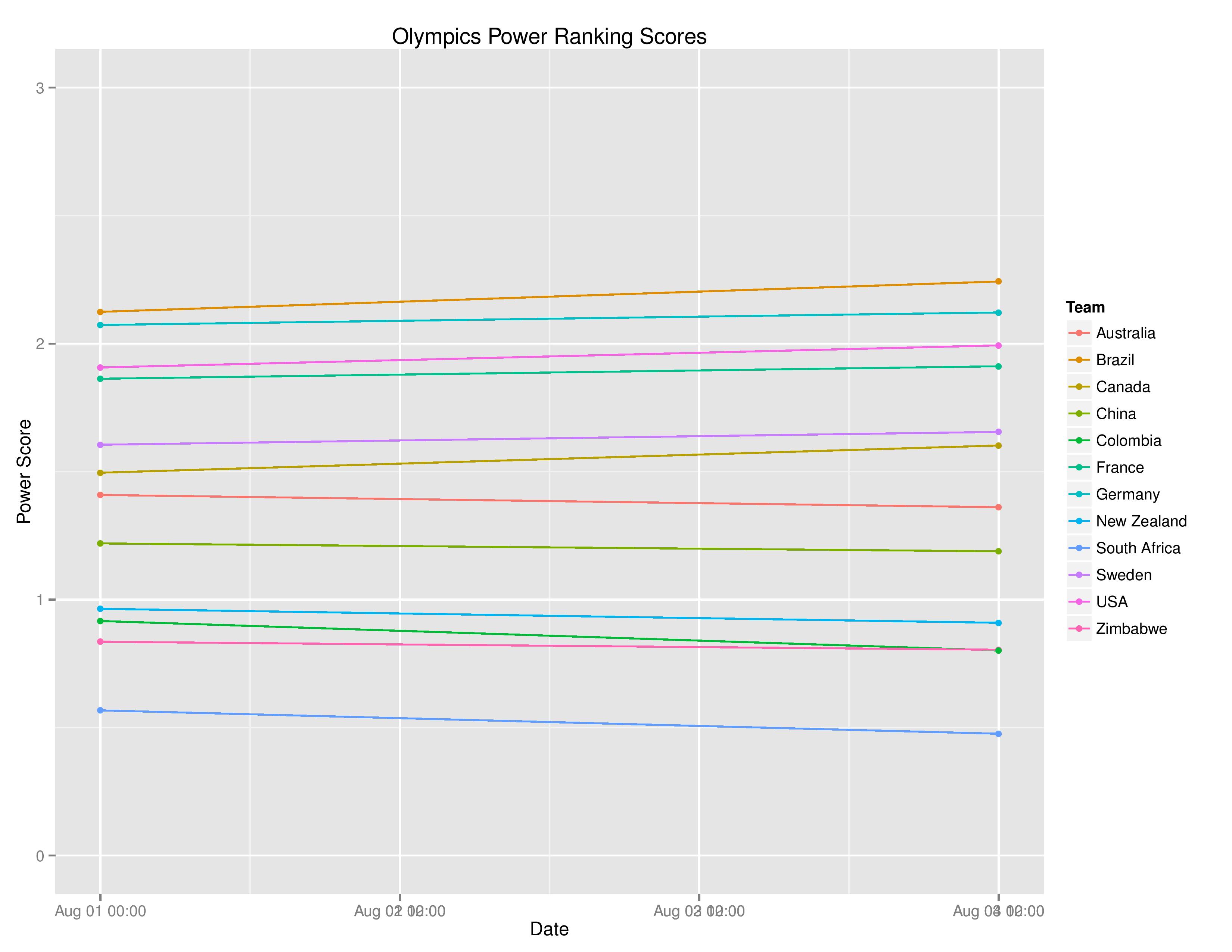
The only teams that changed ranks are Zimbabwe and Colombia. While Zimbabwe’s 6-1 loss to Germany would not normally cause them to go up a rank, SEBA’s expectation of Colombia’s skill declined at a faster rate causing them to fall behind Zimbabwe.
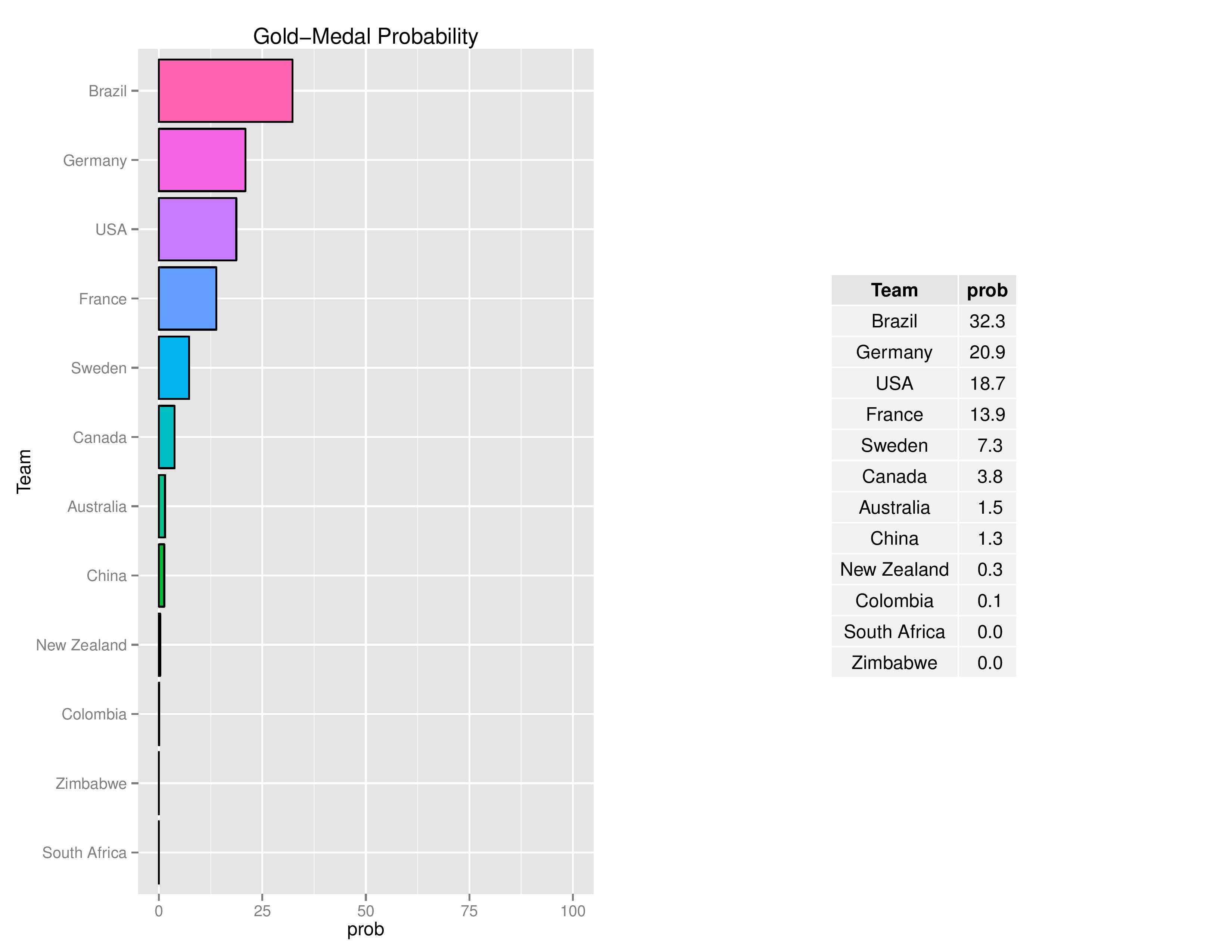
Probability Outcomes
Next demonstrates the probability of winning the Gold Medal for each team.
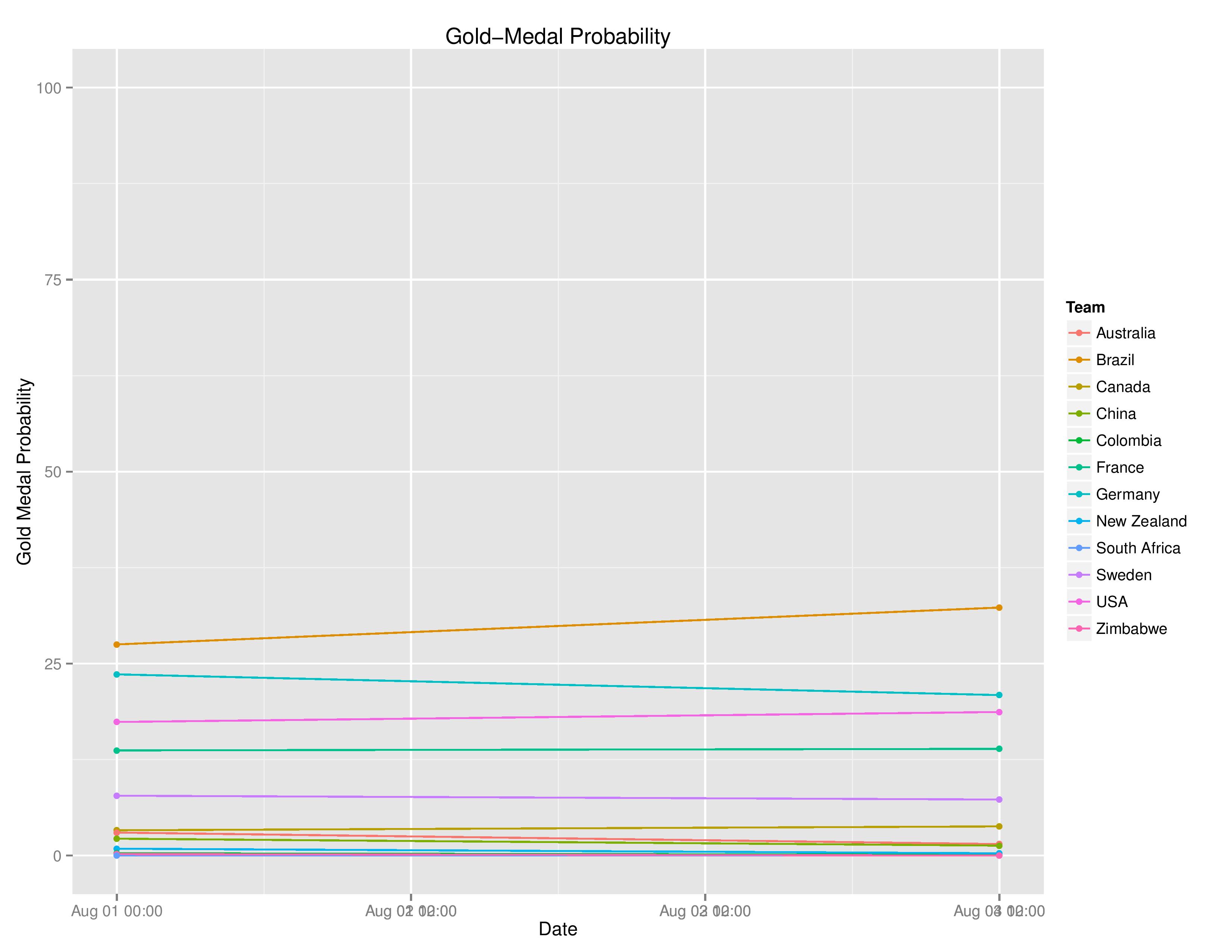
USA’s chances improved slightly to 18.4% from 17.4% with their win over New Zealand. Brazil’s chances increased while Germany’s actually decreased due to their increased probability of a difficult knockout-round-schedule.
Next we see the Gold Medal probabilities changing as the tournament progresses:
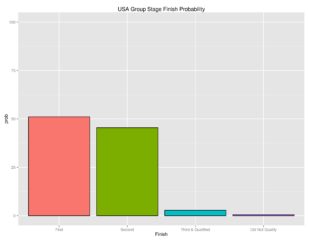
The following is the probabilities for the advancement from the group stage.
USA’s odds went up from 91.9% to 99.4%.
We can now see how the Group Advancement probabilities evolve over time:
Next shows the Group of Death Rankings. This is determined by the All vs. All expectation of points (i.e. every team playing against every team and then averaging the expected points by group).
USA’s team is in Group G, the second-most-difficult of the three groups. The most difficult group is Group F which is composed of Germany, Canada, Australia, and Zimbabwe.
The following is the probabilities of how USA qualifies (or doesn’t) at the end of the group stage:
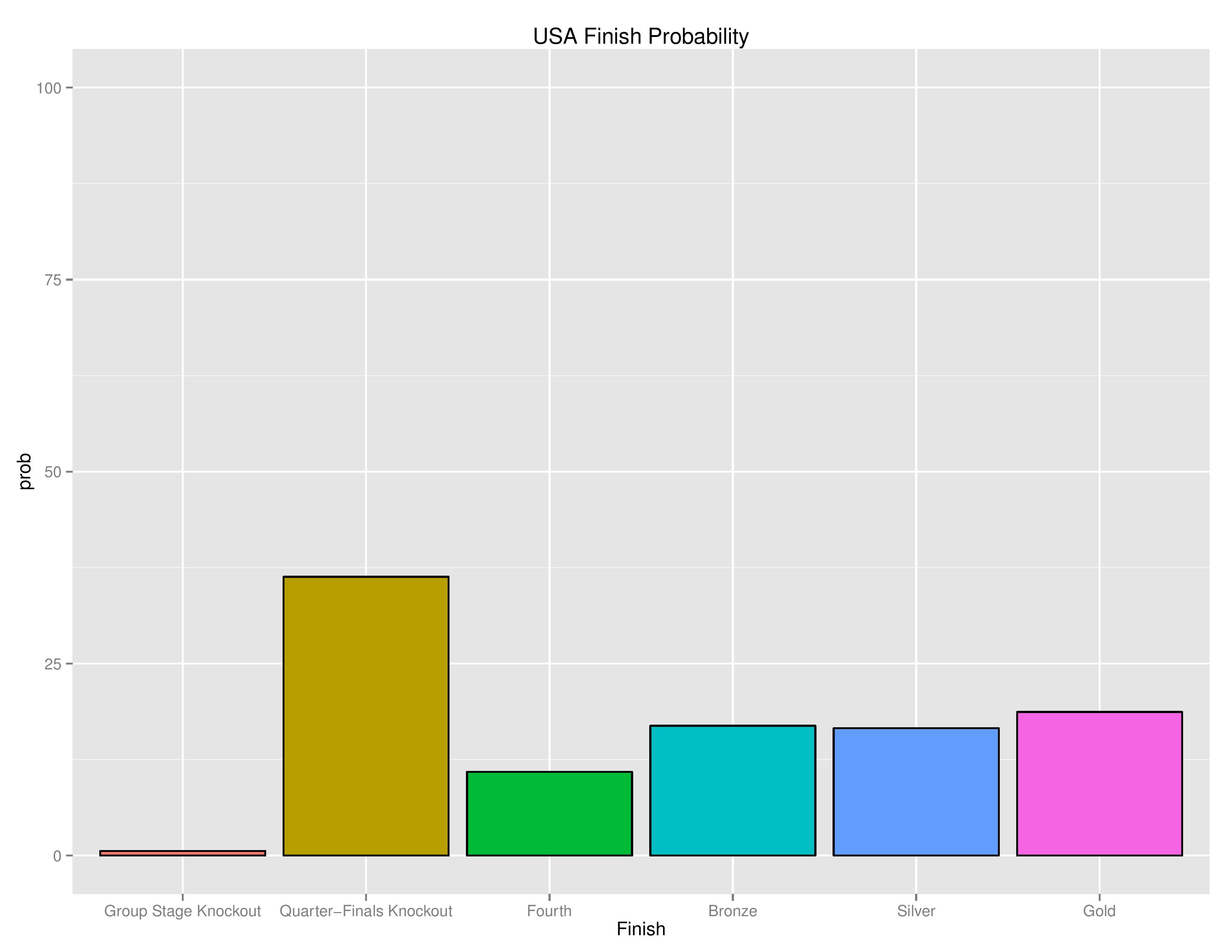
Next is showing USA’s probabilities of all possible outcomes:
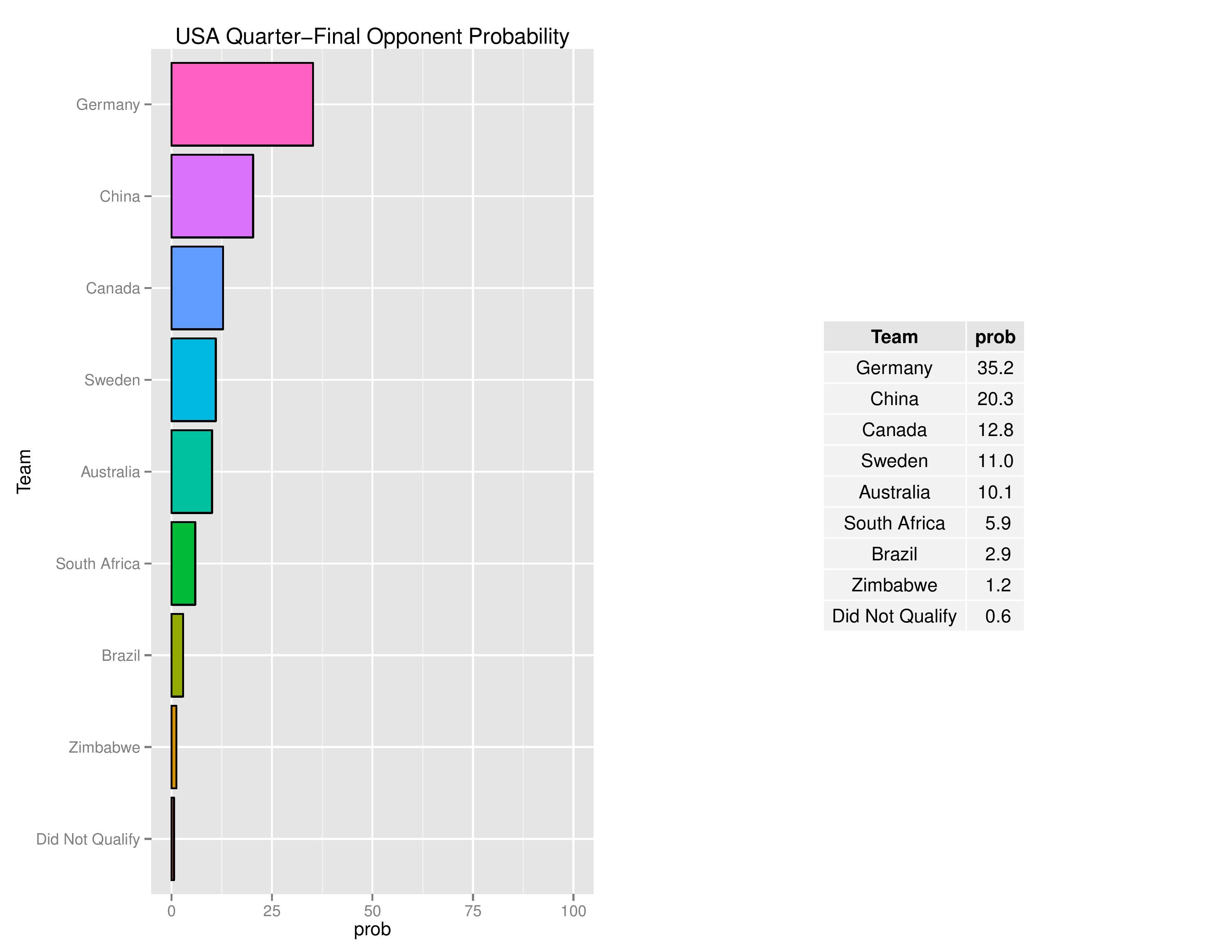
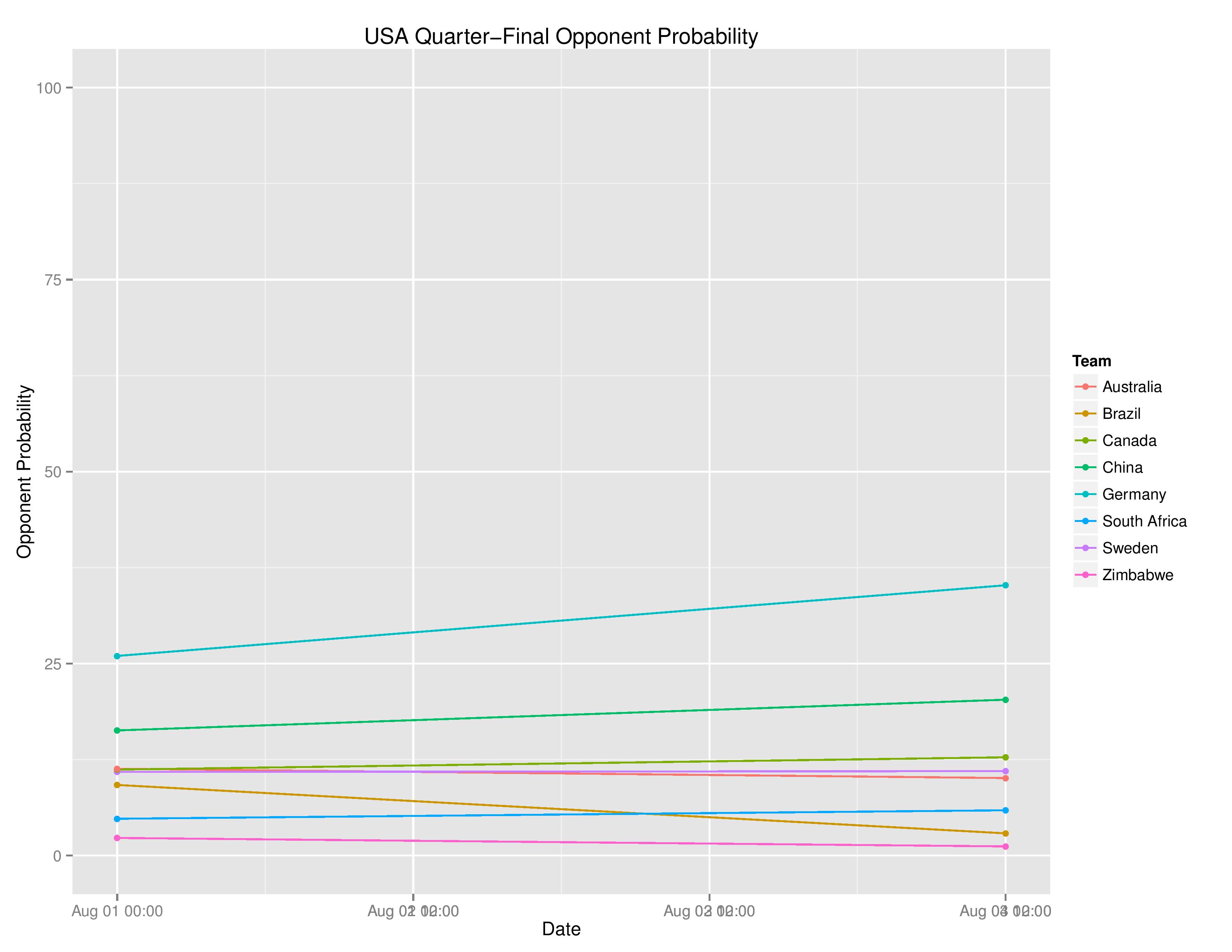
USA’s likelihood of their Quarter-Final opponent is below. As you can see, playing Germany in the quarter-finals is actually the most probable scenario. This would occur if the USWNT finishes the group in 2nd (not all that unlikely with France in the same group) and Germany finishes their group in 1st. Therefore, to avoid playing potentially the best rival in the world in merely the quarter-finals, it is essential that USA win their group to likely play China instead.
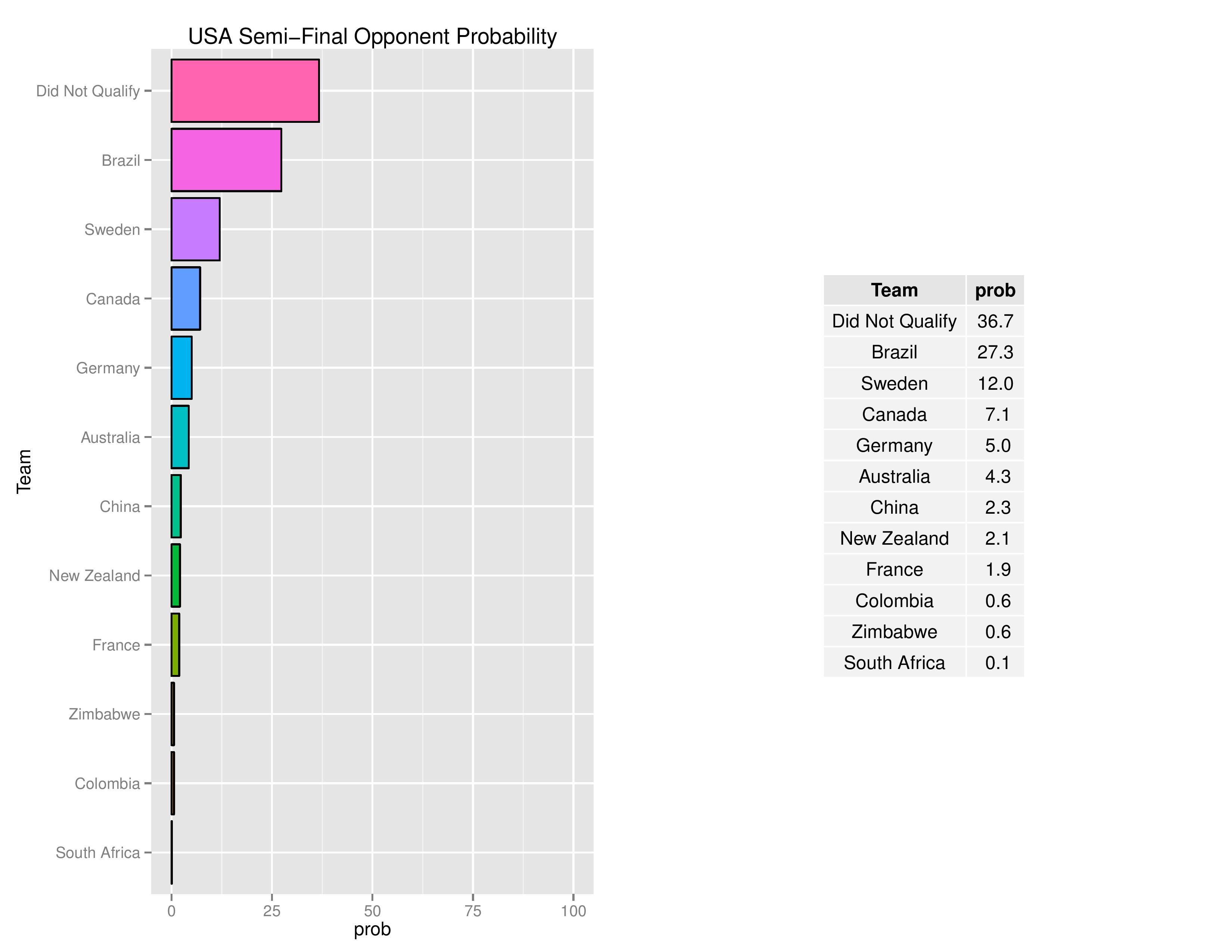
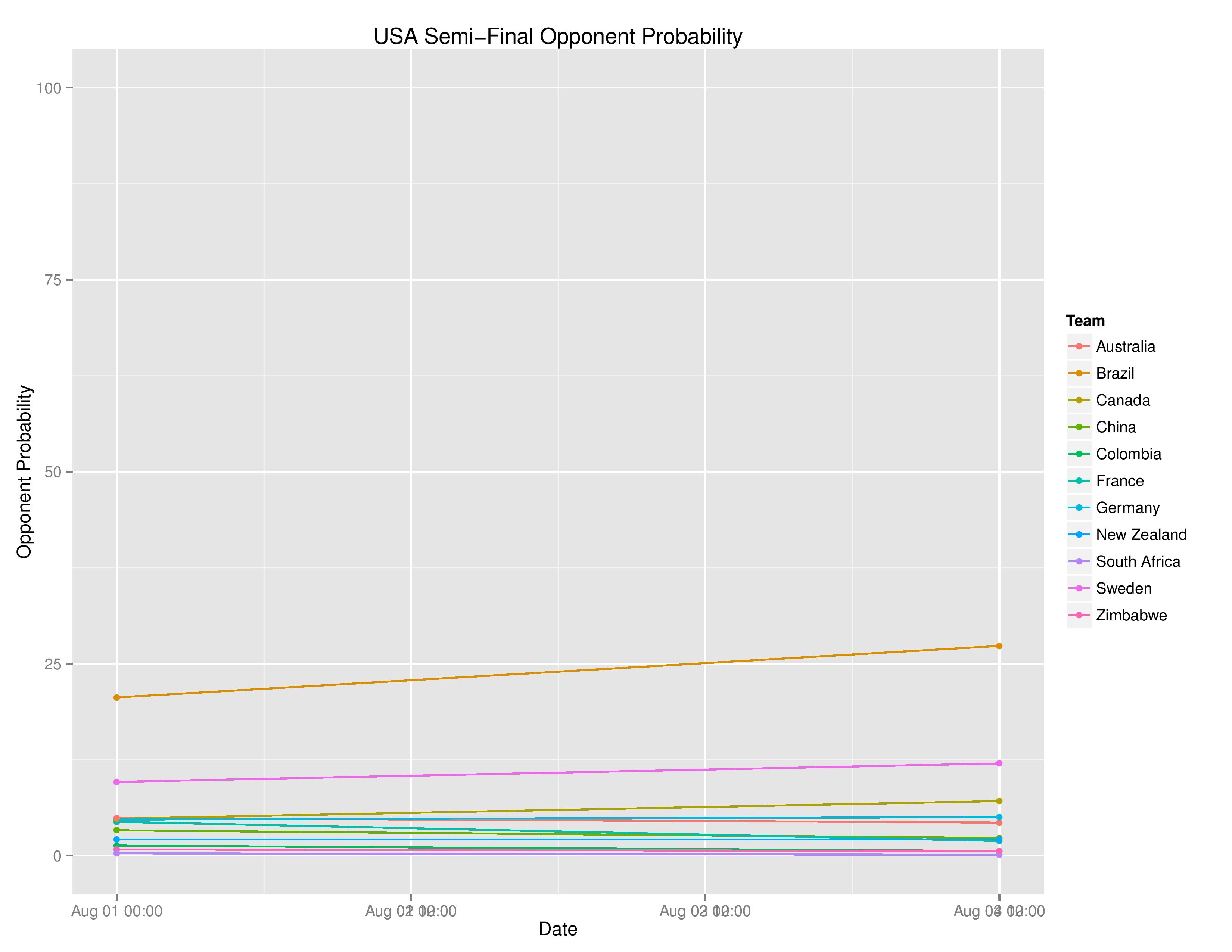
USA’s likelihood of their Semi-Final opponent down below:
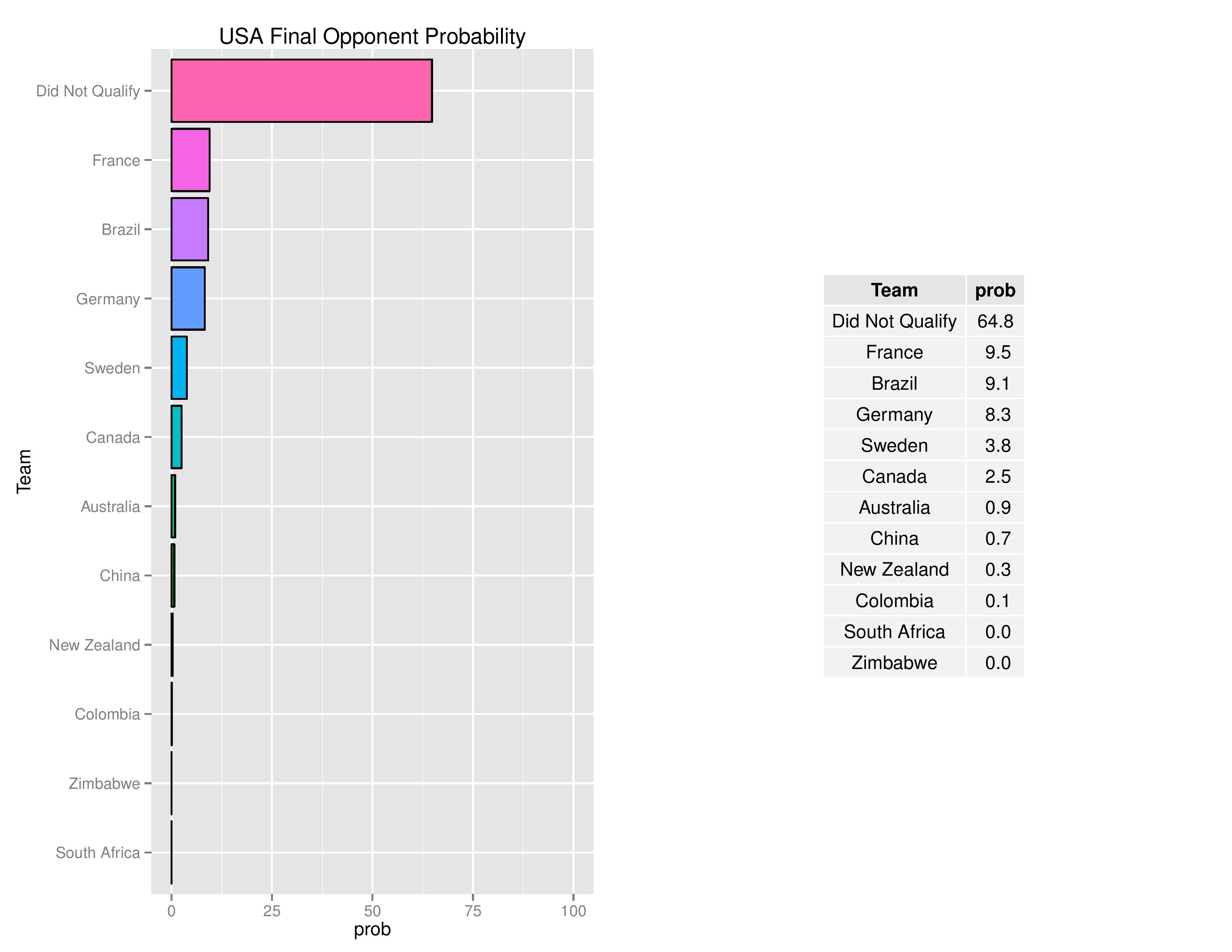
The USWNT’s probabilities of the Final opponent is next:
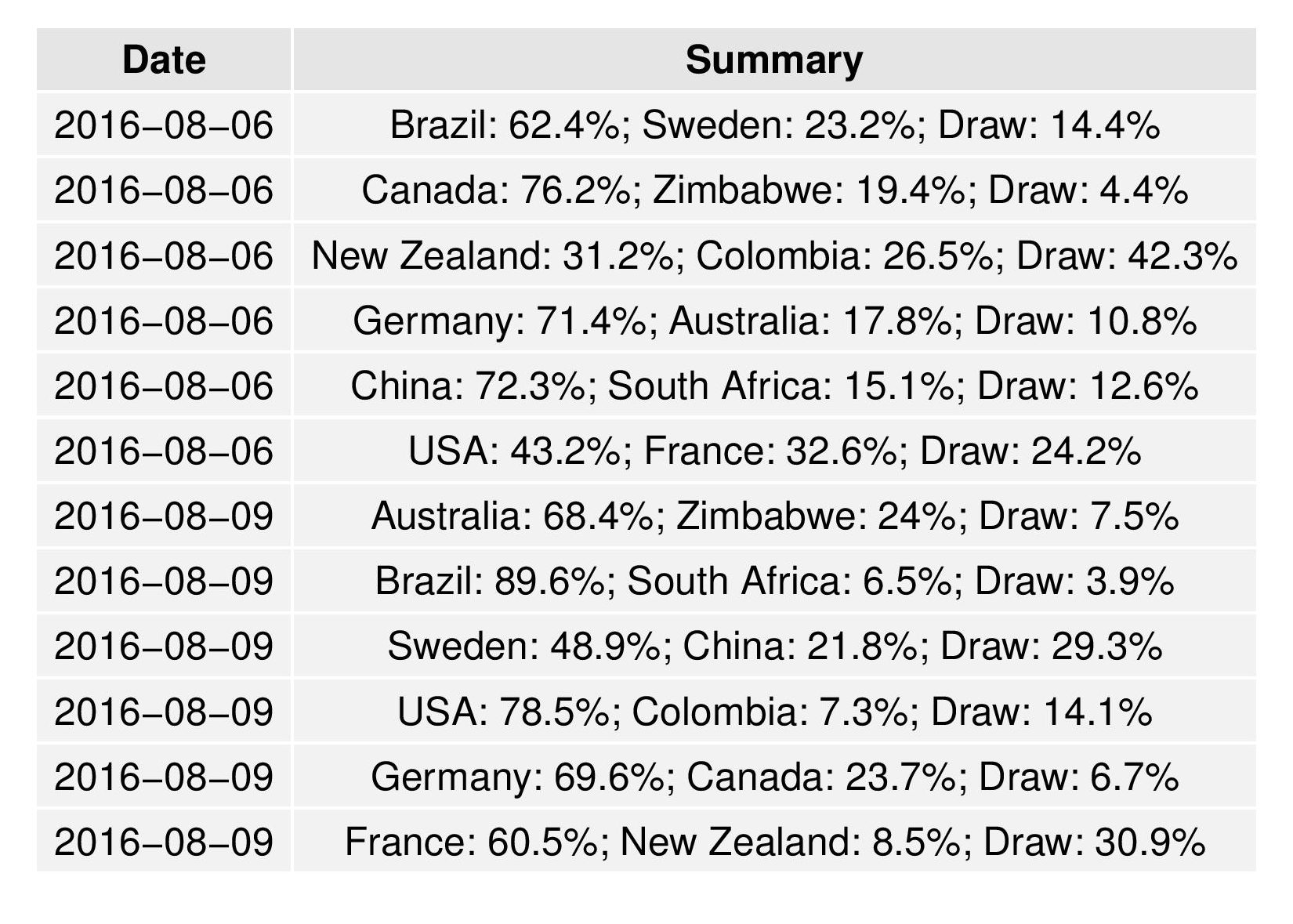
The following shows the upcoming game outcome probabilities:
How the model has changed since Copa America
Other than that this is for Women’s teams, of course, as the base methodologies are the same between Men’s and Women’s competitions.
A key difficulty with assessing national teams’ current form is in properly addressing teams which do not play a large variety of teams (and especially in confederations which do not play outside of their confederation often). Any model, without additional guidance, will treat teams as ‘average’ unless it is certain they are not. When a team from a weak confederations consistently gets wins against weak teams and does not compete against strong teams, the model will unfairly promote them as stronger than they likely are, even more so if those weak teams they beat up on also do not test against strong teams.
FIFA World Rankings tries to account for this by arbitrarily assigning a penalty to some confederations in all their match results. To me, this is a ludicrous practice, as this assumes that all teams from a weaker confederation are weaker merely for their geographic location. This unfairly punishes Big Fish in a Small Pond (like the USMNT and Mexico) and unfairly rewards Small Fish in a Big Pond. If the USMNT or Mexico defeats the top ten European teams in the world, they would still receive less credit than if a similarly-ranked European team did the same.
When I did the Copa America forecasts, I attempted to correct for these small-market-assessments by, instead, placing additional weights on matches where the teams play each other less frequently. While this helped with the desired result of having AFC and other isolated teams decline in the overall rankings, I do believe it was a mistake to instruct the model to place greater certainty on match-ups between teams that play each other less often. Soccer allows for a lot of chance to be involved, so to suggest that a single match-up could be worth the same weight as the summation of a more-frequent match-up (say USMNT vs. Mexico) is to falsely suggest that chance has little effect.
In this model, instead of changing the weights of less frequent match-ups, I include a national team’s isolation metric (based upon whom they play and whom their opponents play) to be a predictive variable. This is not ideal since teams who play fewer confederation-diverse matches are not inherently less skilled, but I believe it to be both necessary and an acceptable choice for assuming that teams who do not compete abroad tend to be weaker.
In addition, an isolation score is calculated for every match (as opposed to the national teams, in general, as described in the previous paragraphs) the model intends to score to represent the volume of information the model has to draw upon in predicting the outcome. It then uses the magnitude of this match-up-isolation-score to regress the result to the mean (bring the predictions closer to a worldwide average outcome) to reflect the added uncertainty we have with the particular match-up. This should also help to restrict the amount of penalty that the previous paragraph’s model additions add to teams which do not travel abroad. They’ll still be marked as weaker, but we’ll be acknowledging how uncertain we are about their ability.

Here’s the television schedule for broadcasts of soccer games at the 2016 Summer Olympics in Rio de Janeiro.