Below are the updated season forecasts using data from games through August 20.
Power Rankings
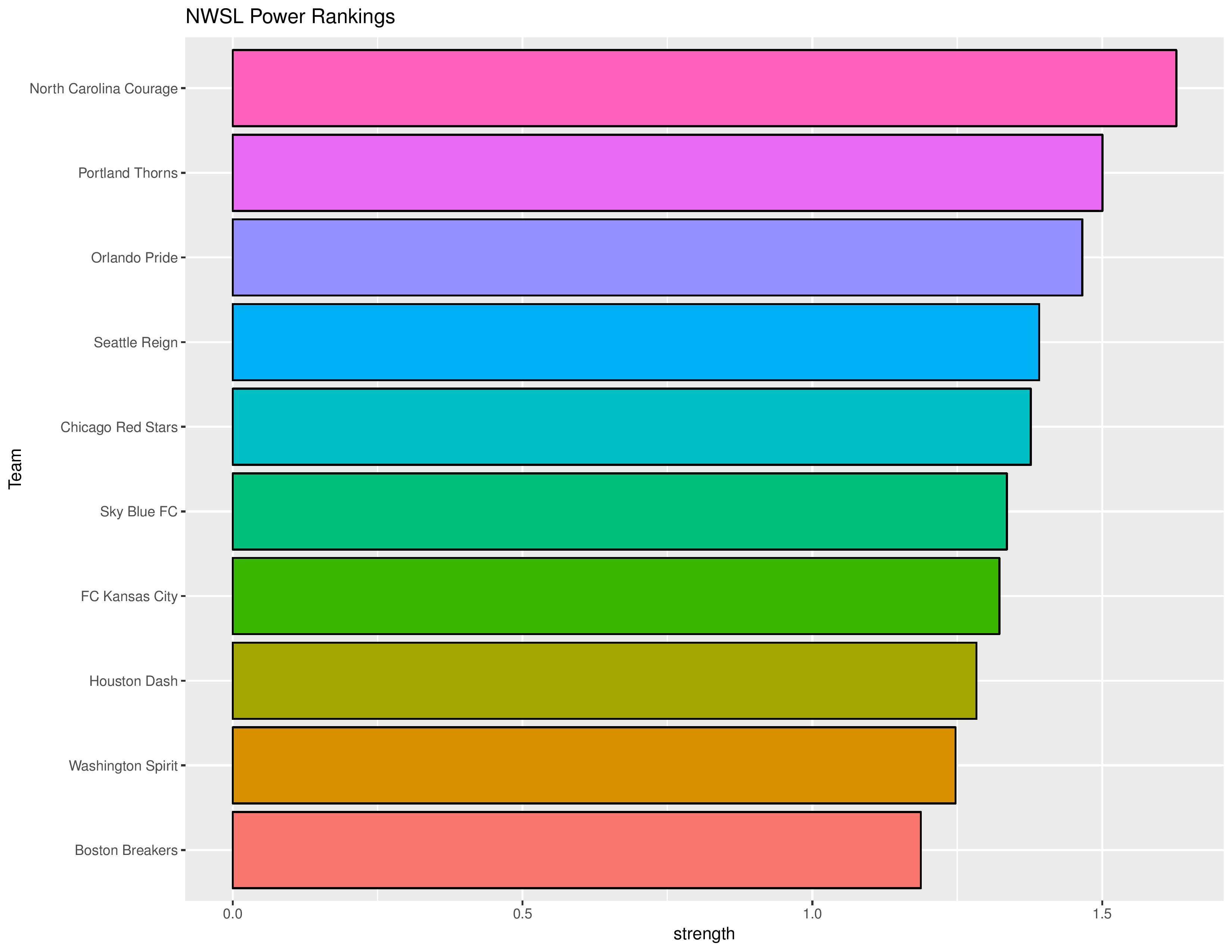
The “Power Rankings” we concoct are the “strength” of the team according to its competitive expectations. They are computed by forecasting the expected points (3 x win probability + 1 x draw probability) against every other MLS team – both home and away – and taking the average per team.
SEBA has the Union declining from 13th to 14th.

For those interested in how Philadelphia’s matches are weighted in the model (especially if skeptical about why SEBA’s rankings can be different from other outlets):
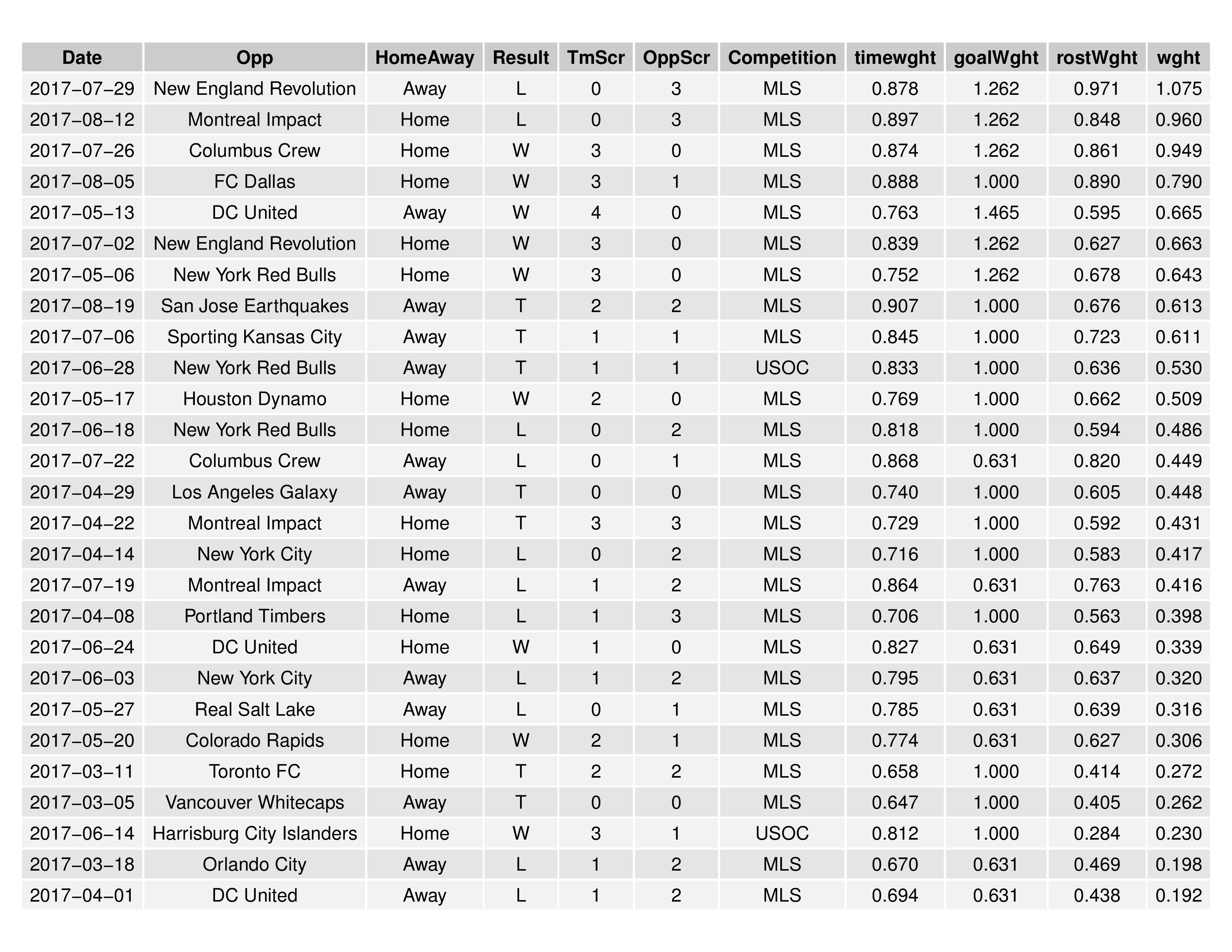
‘wght’ is the actual weight value used in the model, which is a combination of the ‘timewght’ (how long ago the match occurred), ‘goalWght’ (how much luck could have influenced the match result, as indicated by the goal differential), and ‘rostWght’ (how similar the roster deployments for both teams were compared with current trends).
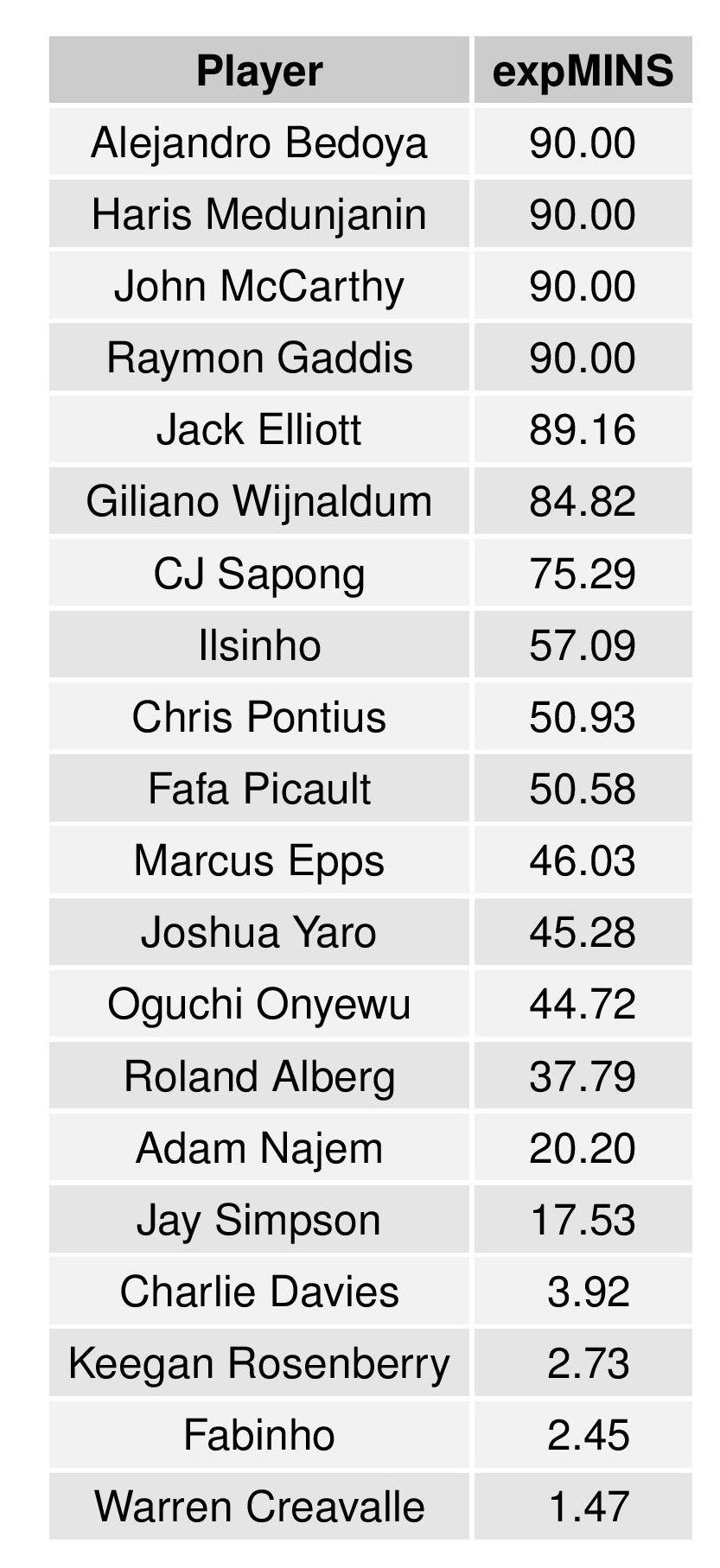
For comparison, the current roster expectations for maximum weight for the Union are currently:
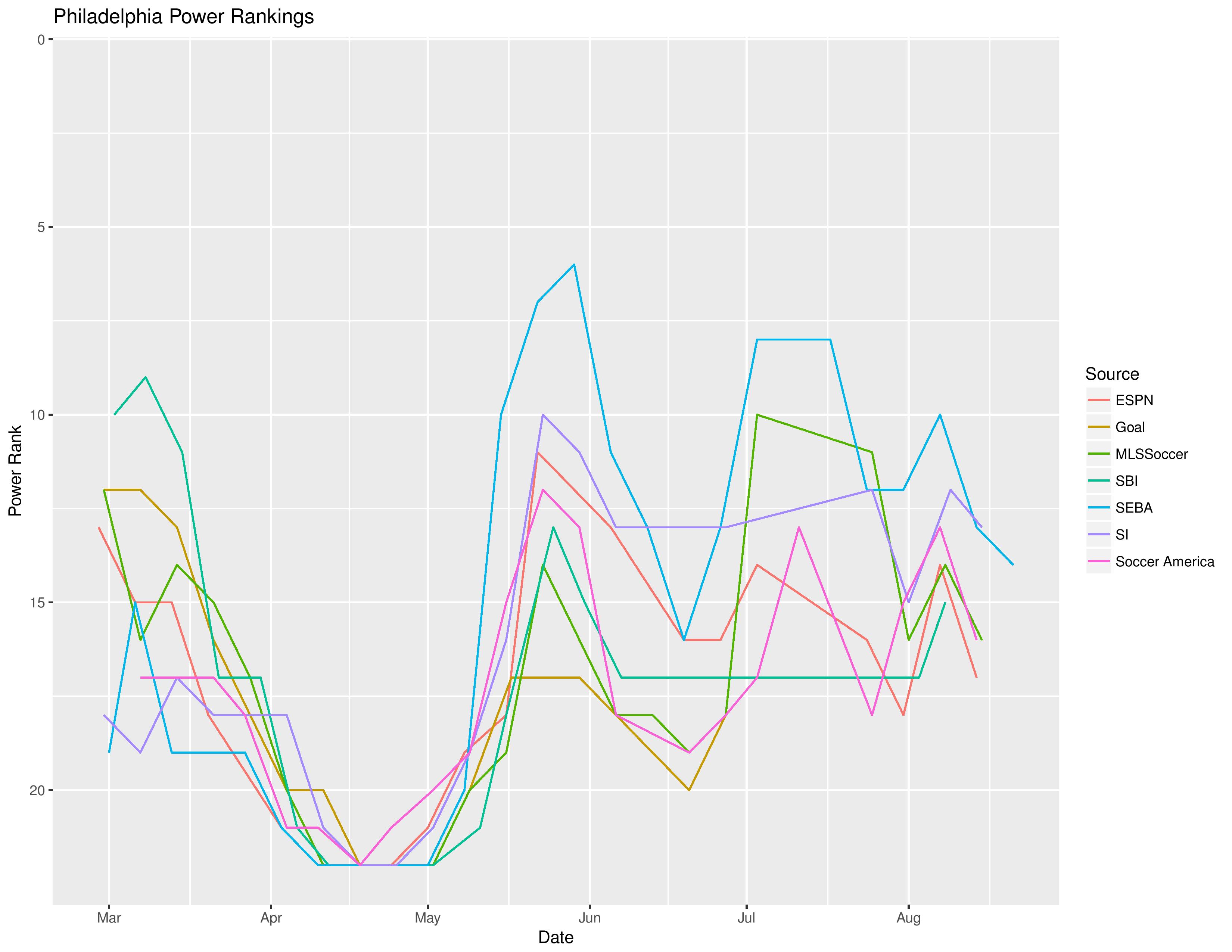
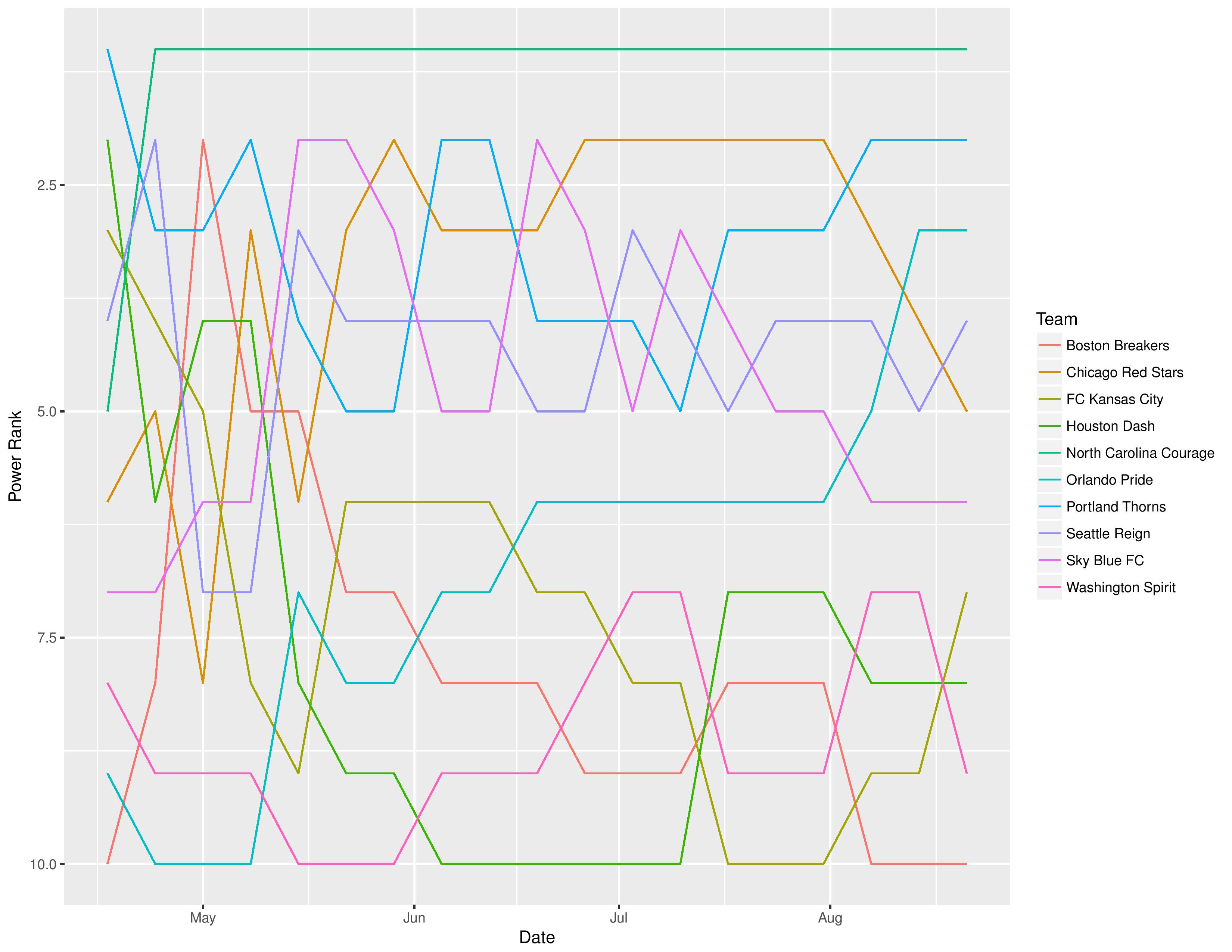
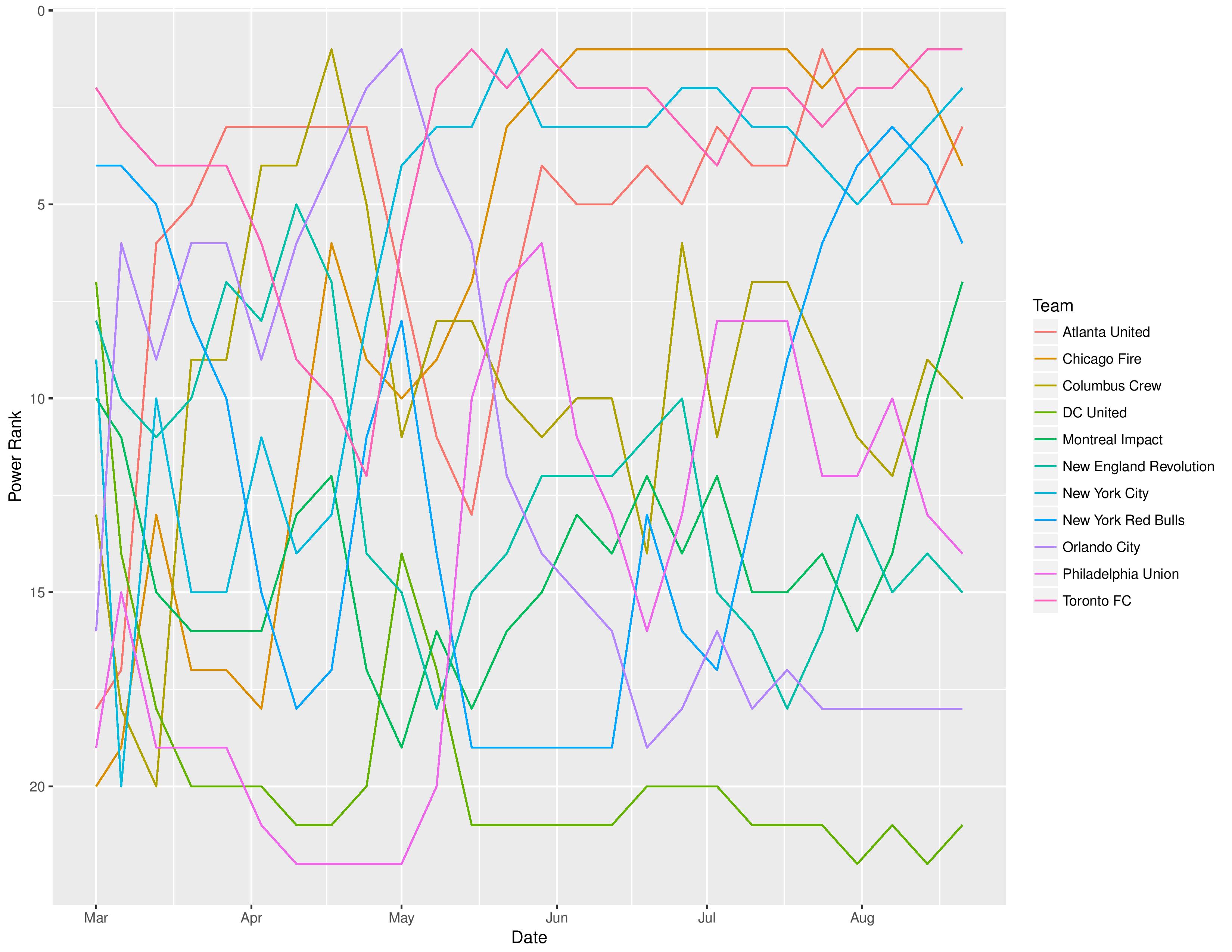
The following shows the evolution of SEBA’s power rankings for the MLS Eastern Conference over time:
Playoffs probability and more
Philadelphia’s playoffs odds have decreased from 2.6% to 1.9%.

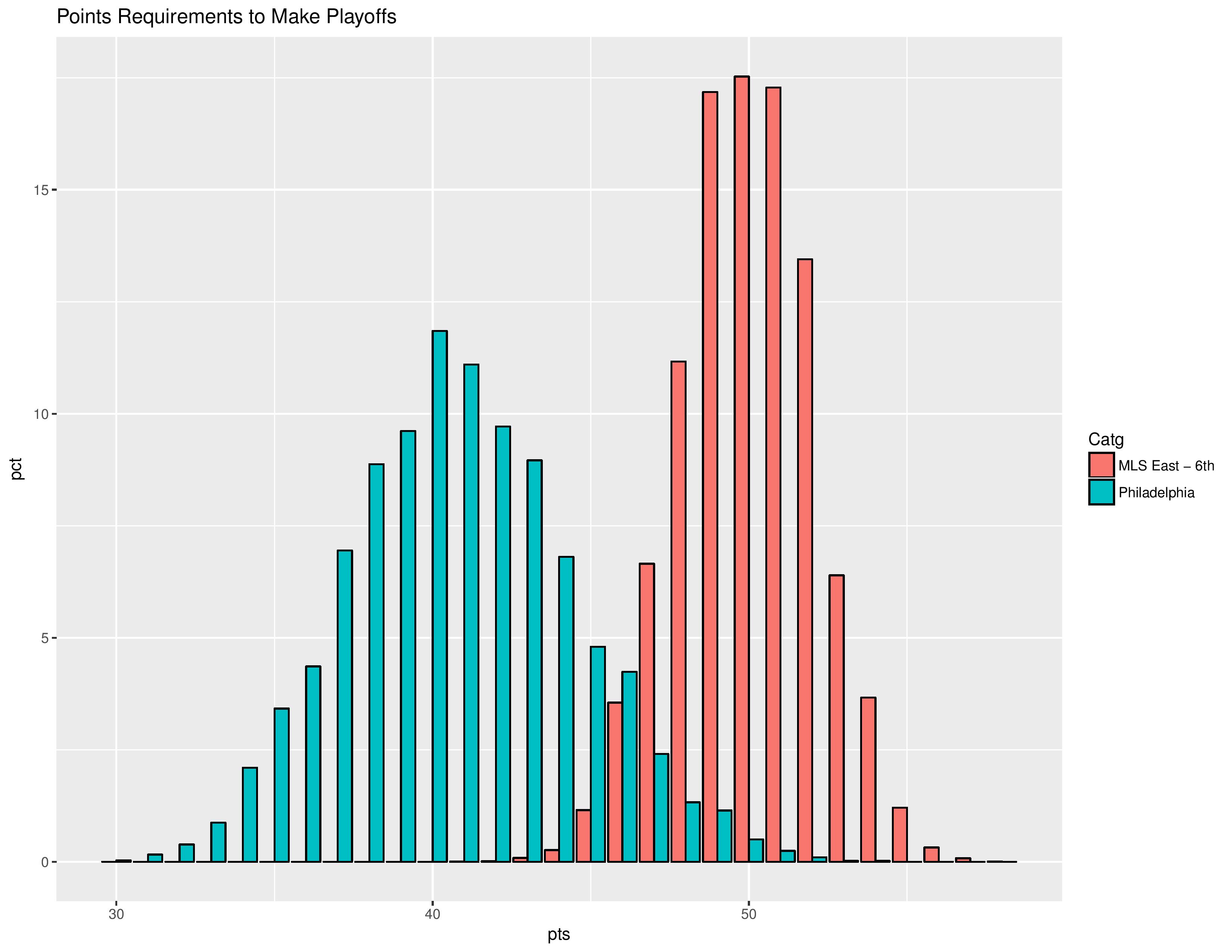
The following shows the simulation distribution for the points earned by the sixth place MLS East club as well as the simulation distribution of points that Philadelphia is expected to earn.
Tiebreakers aside, the Union make the playoffs when >= this MLS-East-6th value.
The most common number of points required to make the playoffs in the East’s 6th slot has increased from 49 to 50 while the most common number of points simulated for the Union remains at 40.
In part, clubs that score a lot of goals are given an advantage in MLS Cup due to the two-leg aggregate goal format of the conference semi-finals and conference finals. This gives those clubs a better chance at notching large victories which carry over.
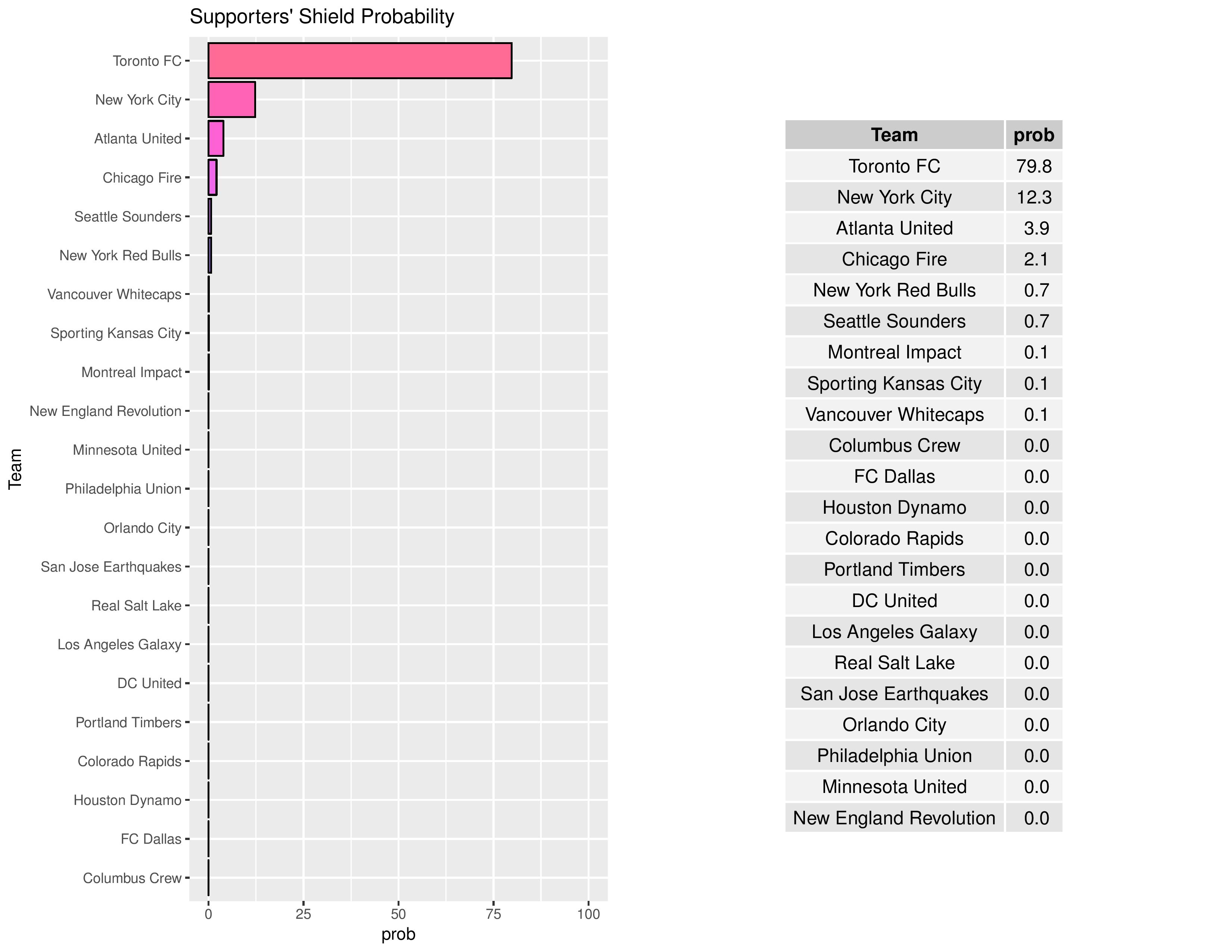
The Union’s chances of winning the MLS Cup remains at practically zero.

In the U.S. Open Cup, poor teams with a higher propensity to earn a draw are given an advantage as they are more likely to reach penalty kicks, which are a complete tossup. Conversely, good teams with a higher propensity to earn a draw have a disadvantage for the same reason.
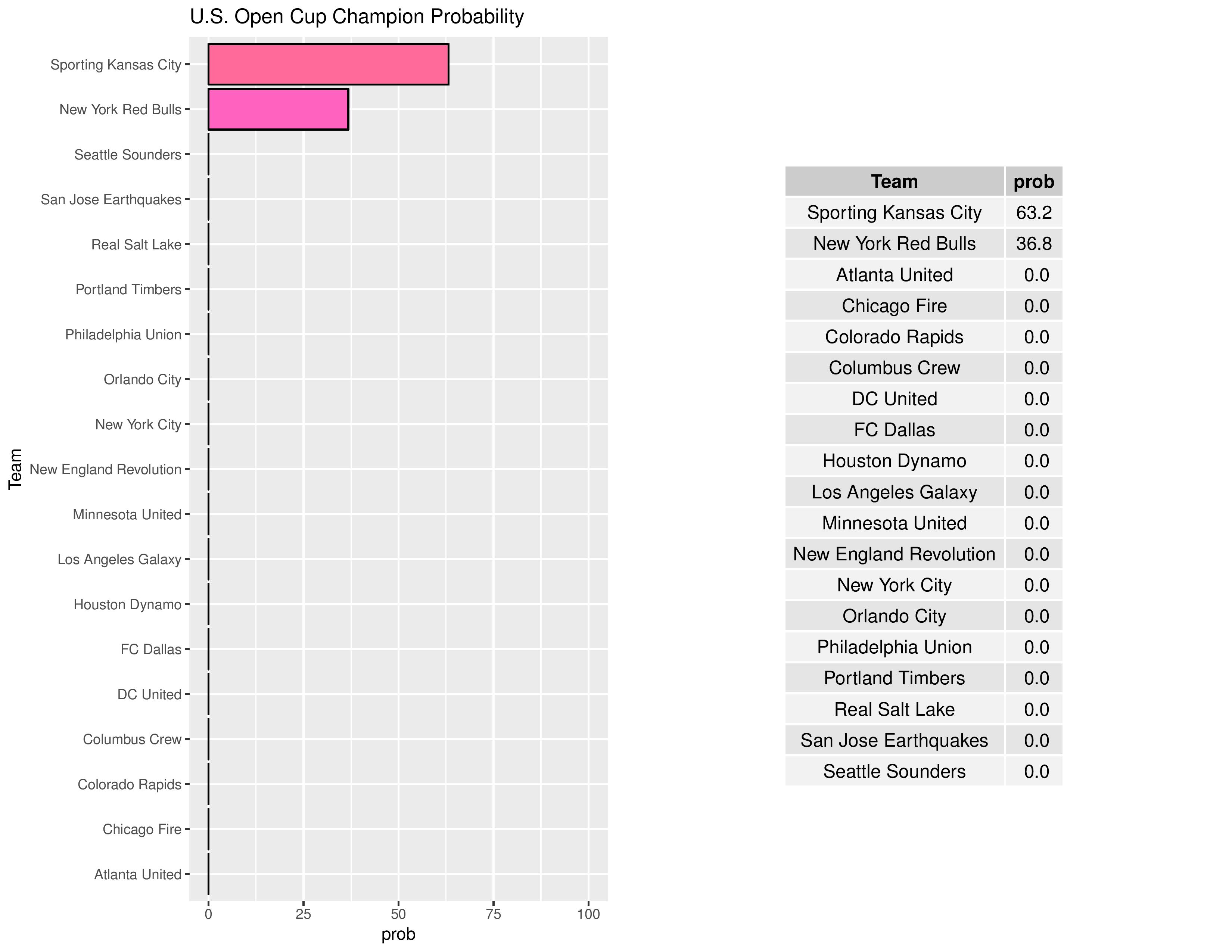
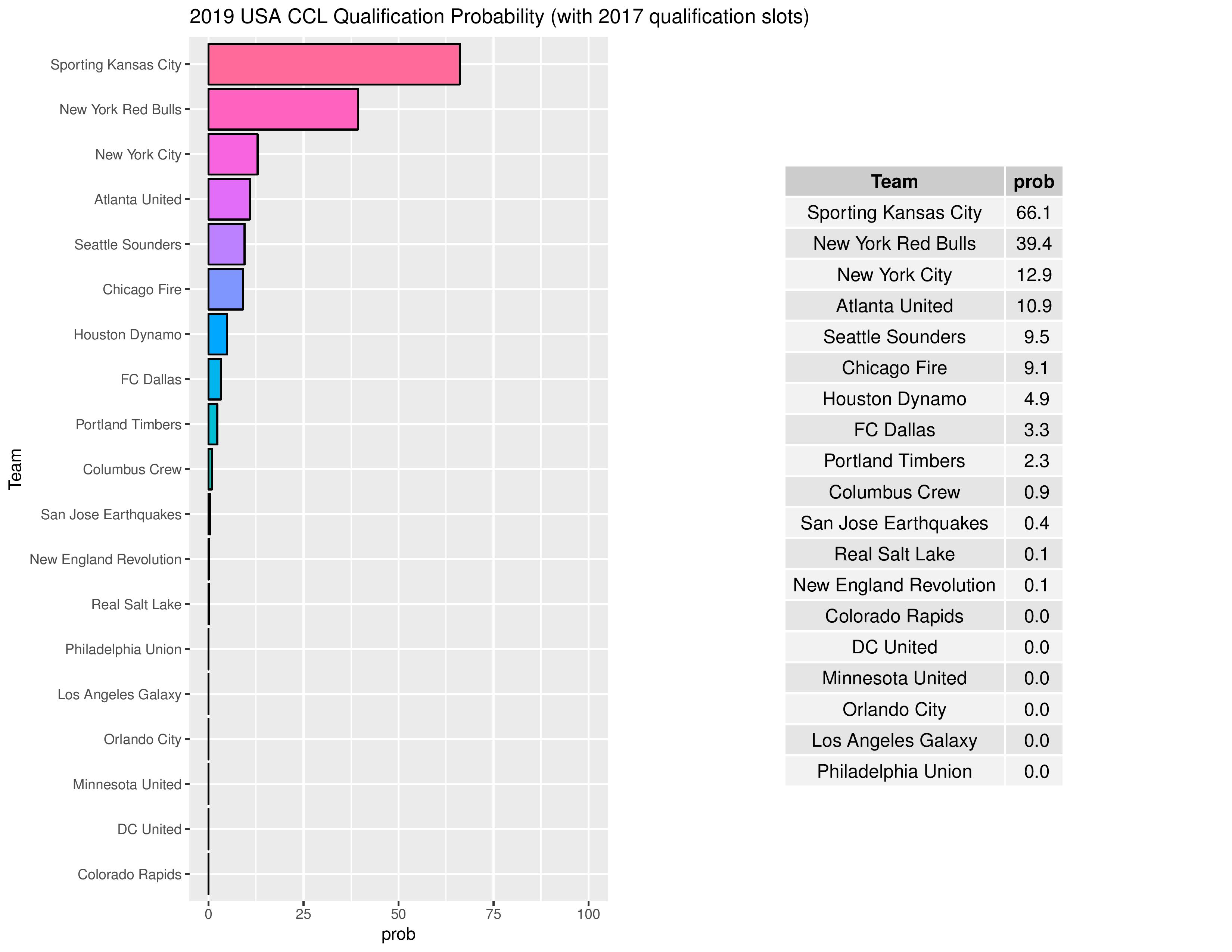
Philadelphia’s chances for qualifying in 2017 for the 2019 edition of the CONCACAF Champions League remain at practical zero.
Over time, we can see how Philadelphia’s odds for different prizes have changed.
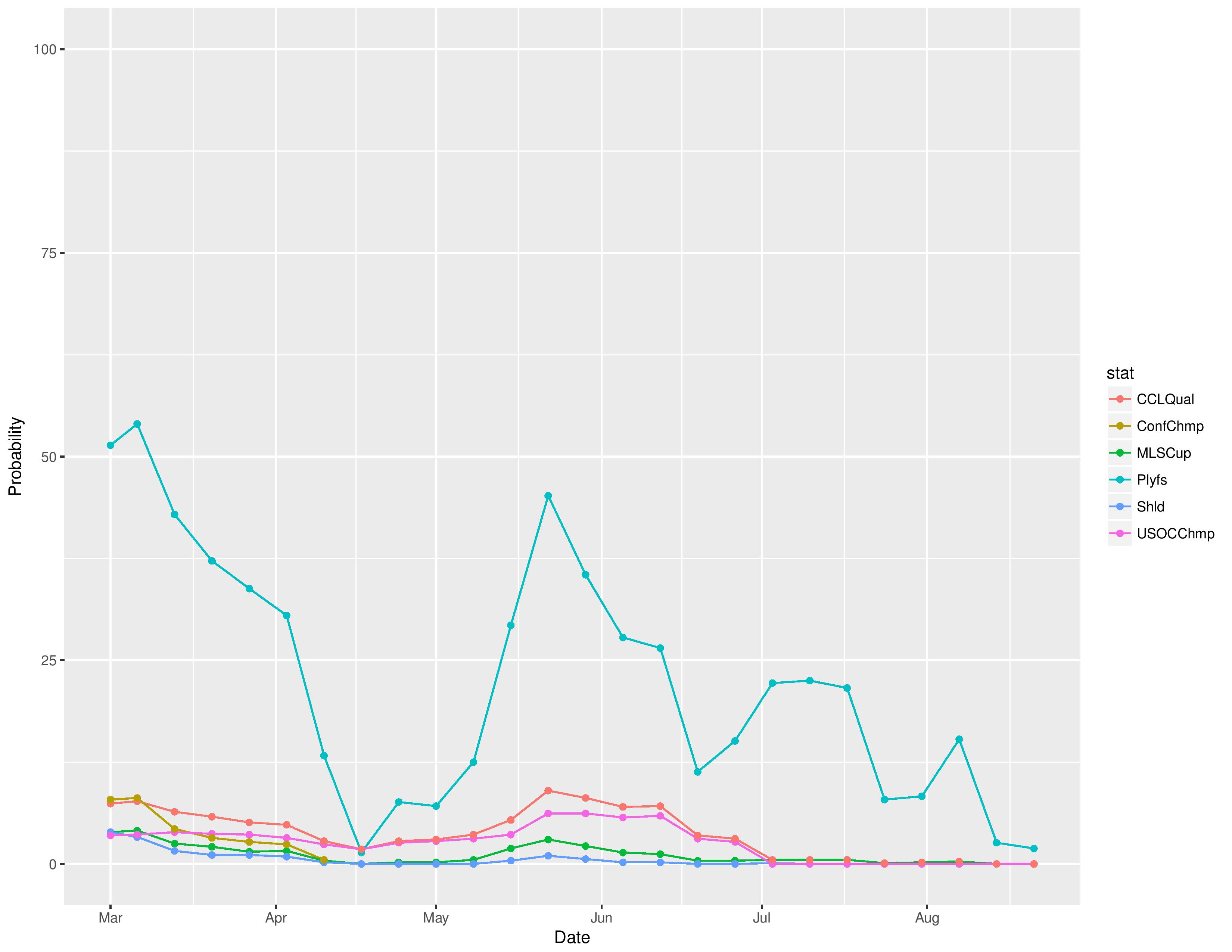
The following are probabilities for each category of outcomes for Philadelphia:
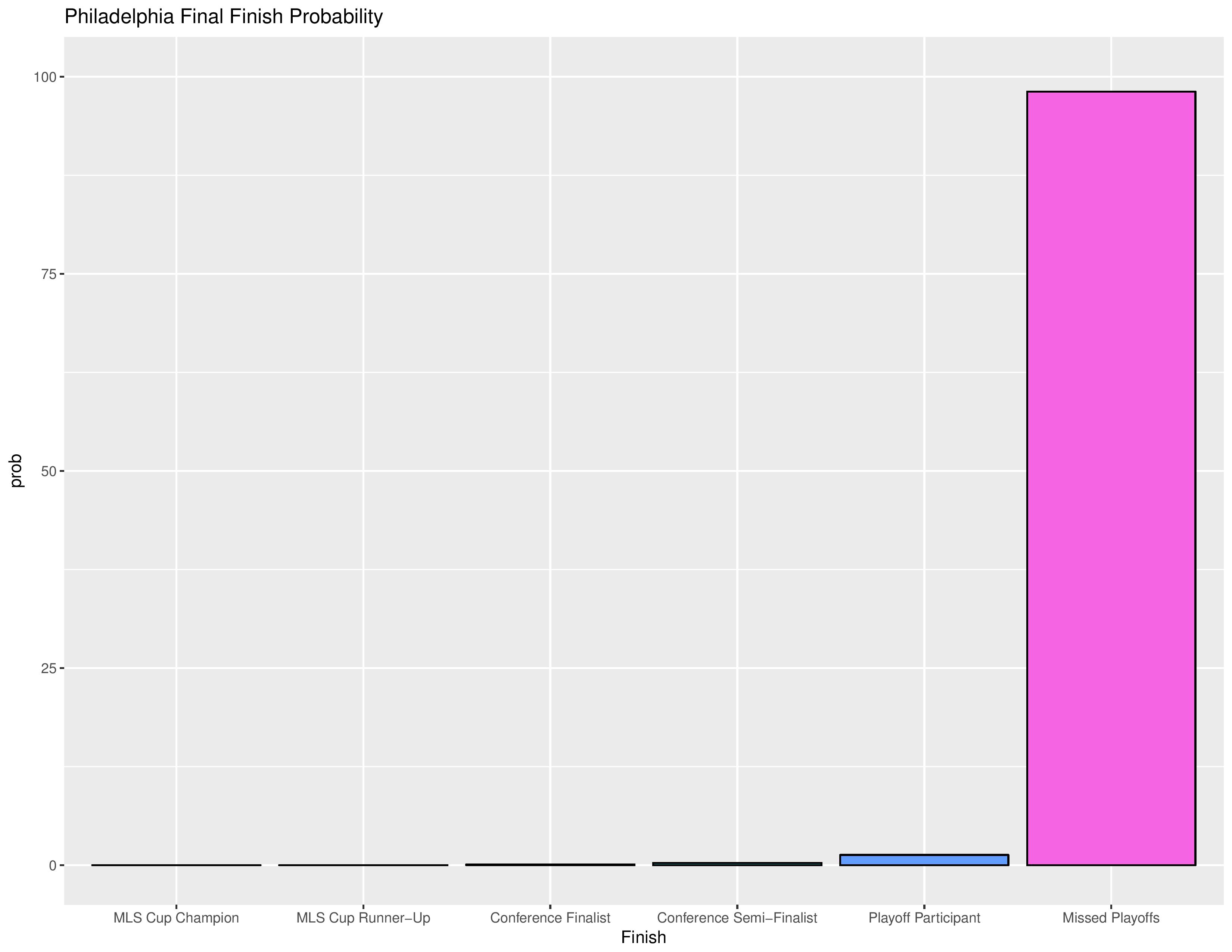
The following shows the probability of each playoff ranking finish.

The following shows the summary of the simulations in an easy table format.

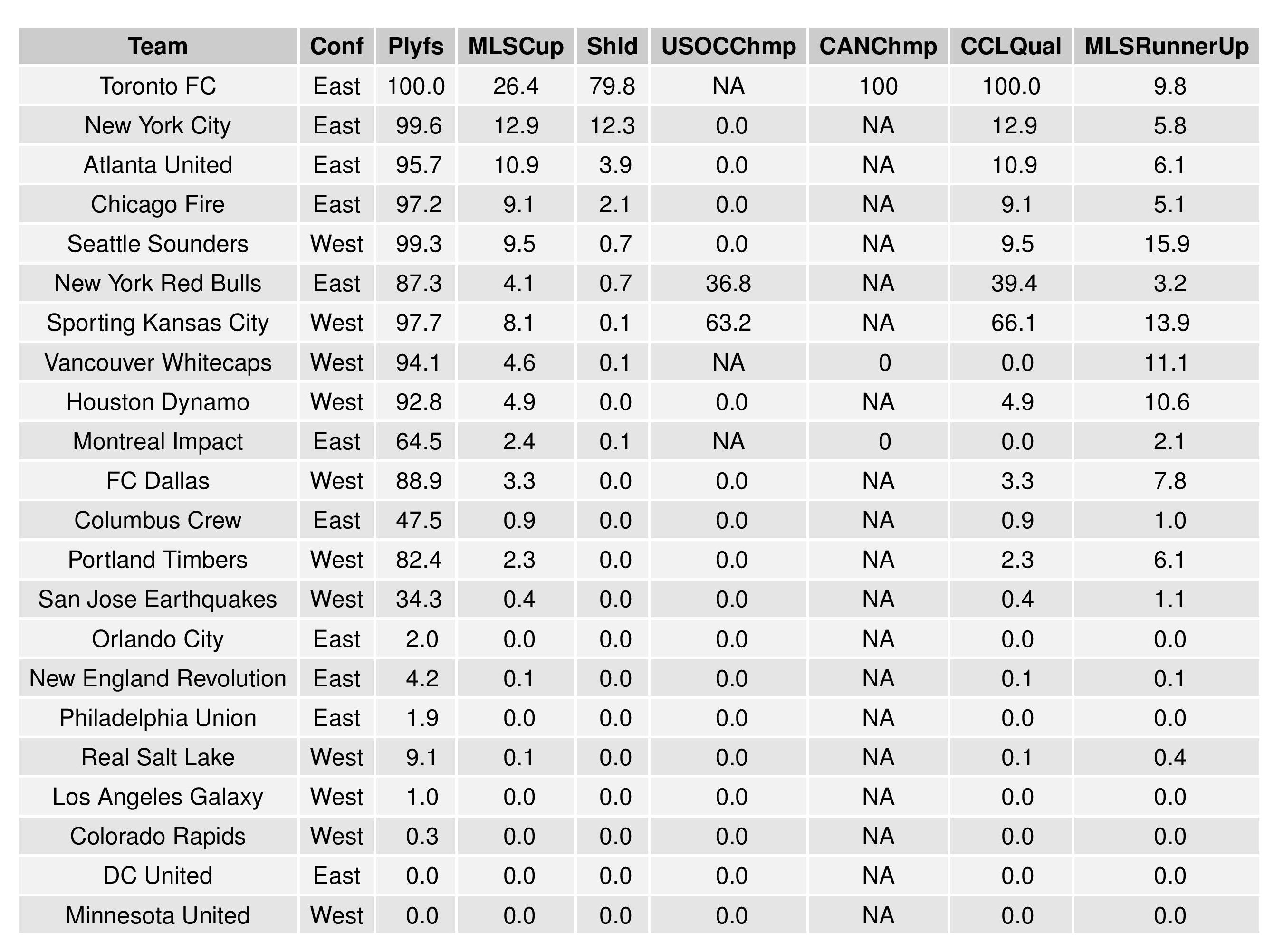
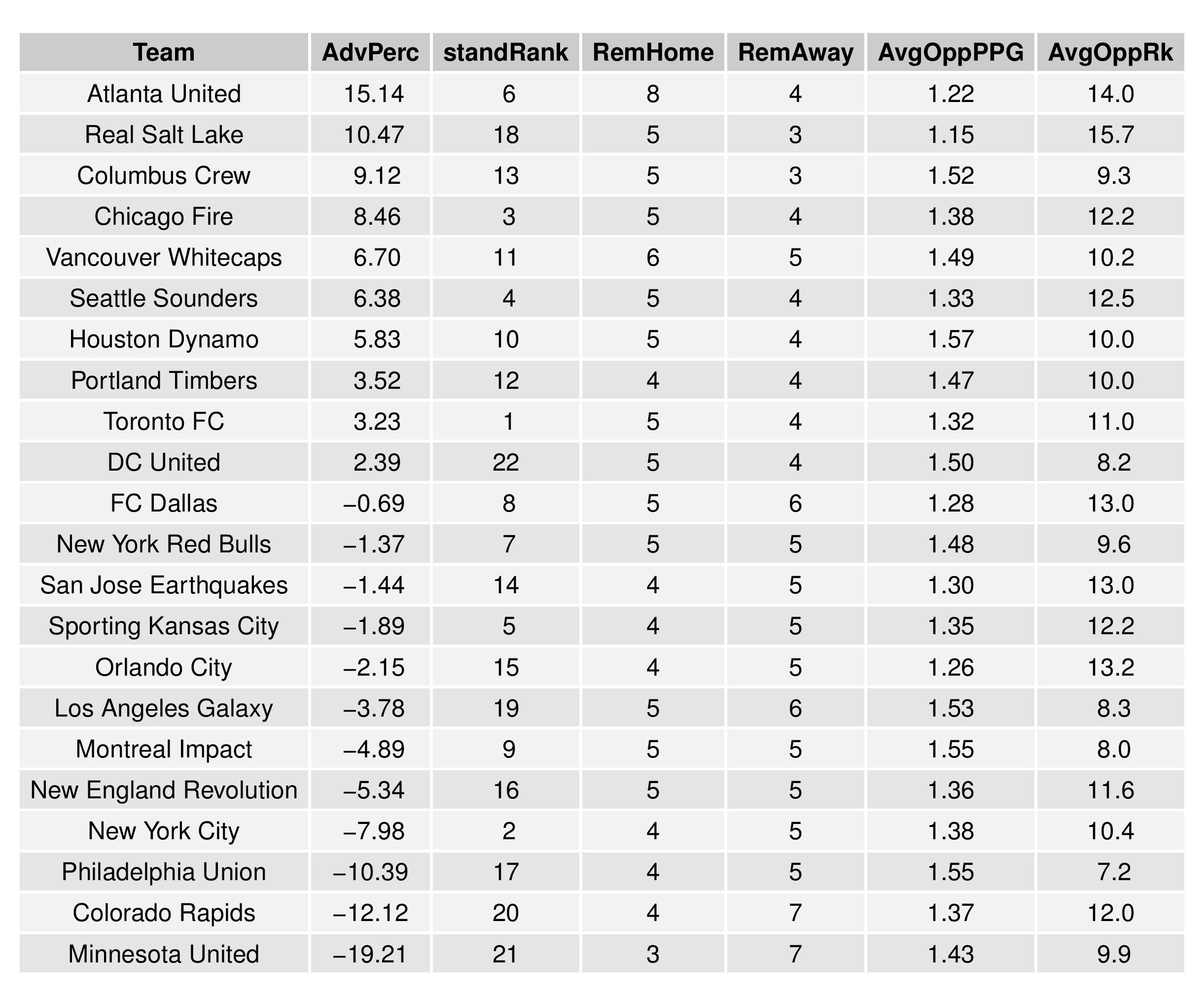
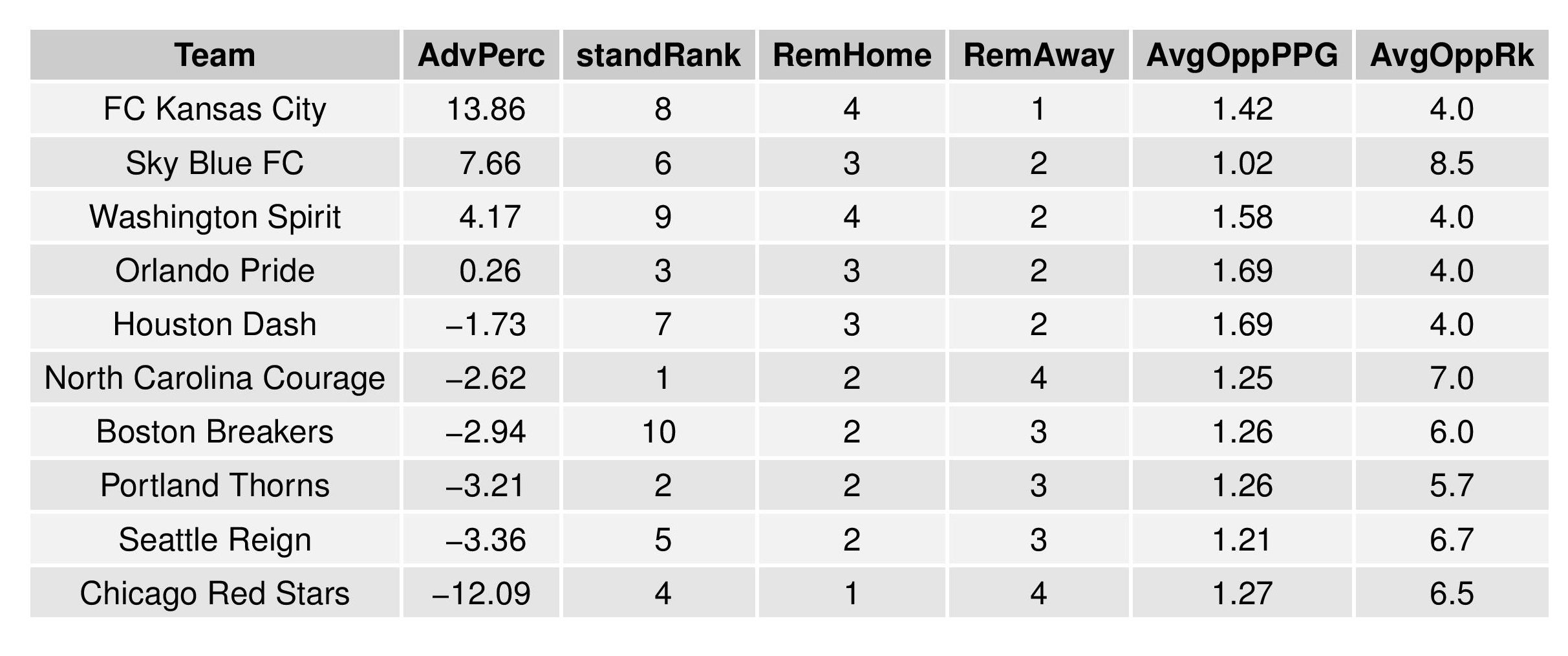
Next, we show how the Remaining Strength of Schedule affects each team.
The “Points Percentage Advantage” shown on the X-axis represents the percentage of points expected over the league average schedule. This “points expected” value is generated by simulating how all teams would perform with all remaining schedules (and therefore judges a schedule based upon how all teams would perform in that scenario).
In short, the higher the value, the easier the remaining schedule.

Accompanying the advantage percentage in the following table is their current standings rank (right now ties are not properly calculated beyond pts/gd/gf; I may fix that, but maybe not for a while), the remaining home matches, the remaining away matches, the current average points-per-game of future opponents (results-based, not model-based), and the average power ranking of future opponents according to SEBA.
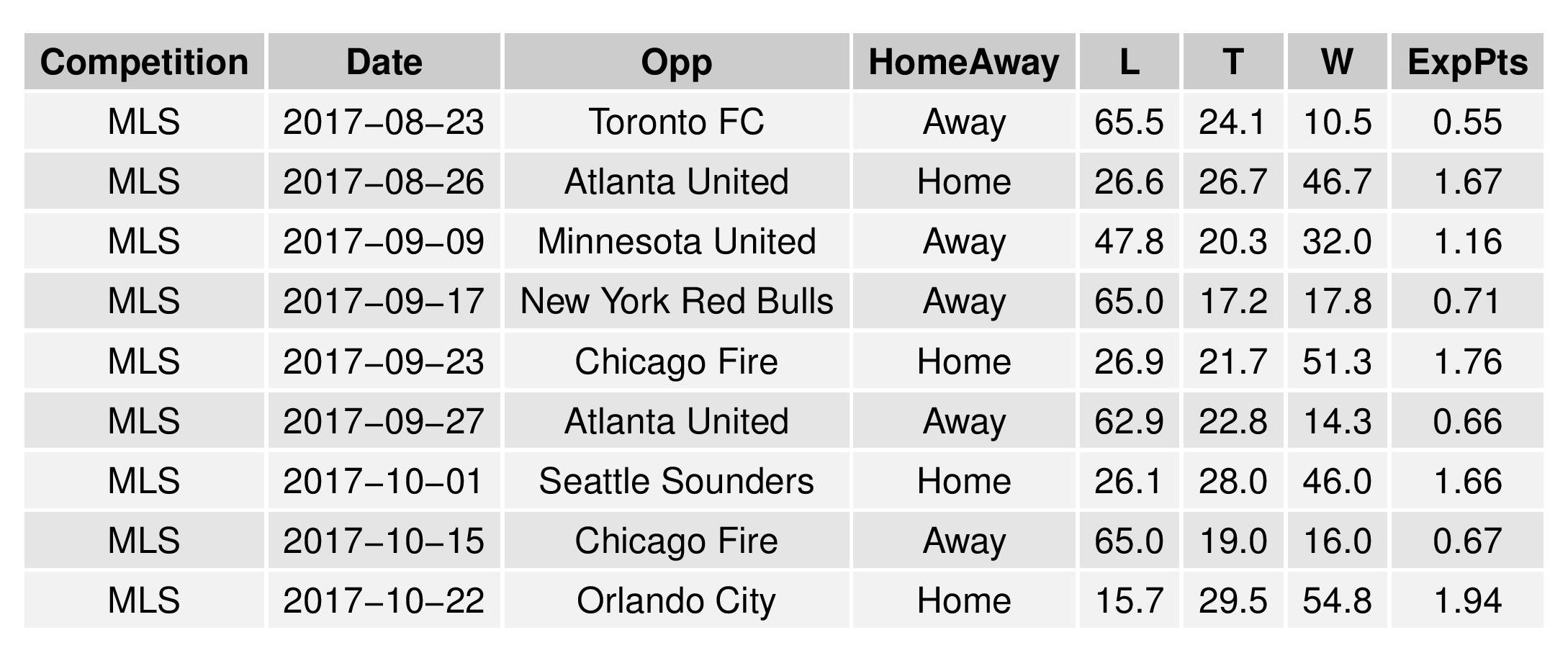
The following shows the expectations for upcoming Philadelphia matches:
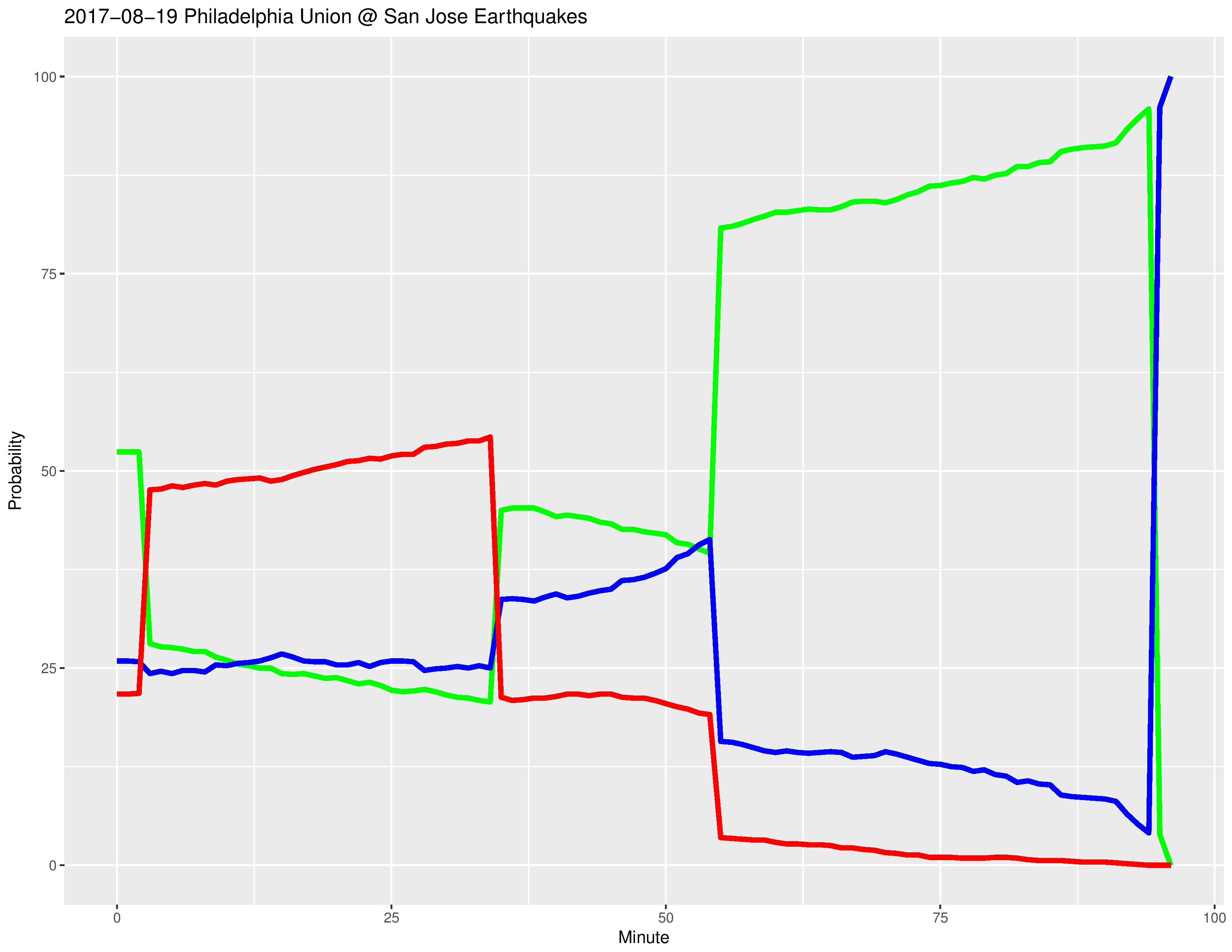
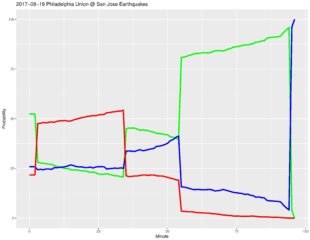
Last Game Probability Chart
This model finally incorporates changing team statistics due to subs and yellow/red cards.
For the following, the green line represents the odds of a win, the blue line the odds of a tie, and the red line the odds of a loss.
The following shows the changing proportion of Philadelphia’s probability of scoring goals compared with their opponent’s. This proportion can only change due to subs, yellow cards, and red cards.
*For example, a value of 2 means that Philadelphia is twice as likely to score as their opponent. A value of 0.5 means that Philadelphia is half as likely to score as their opponent.
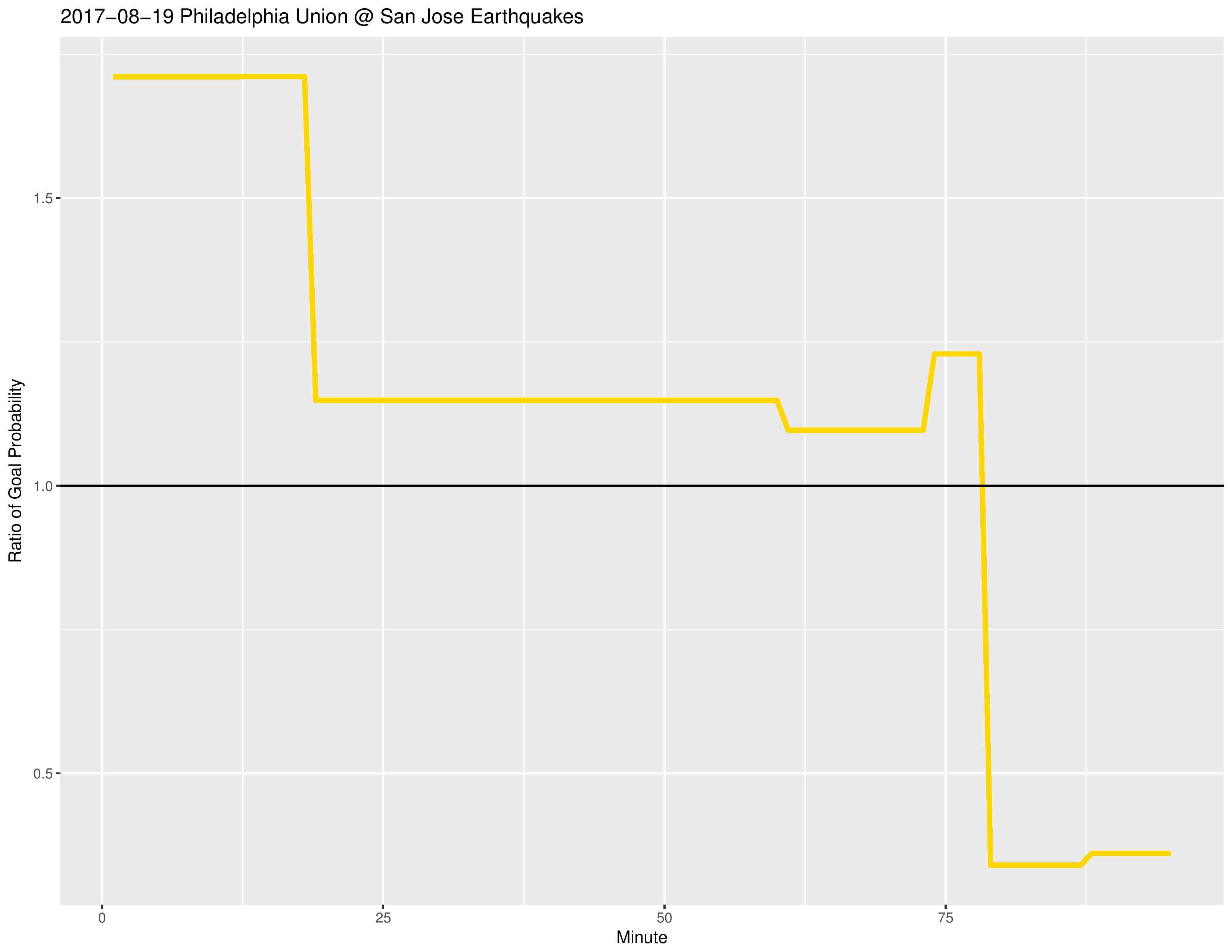
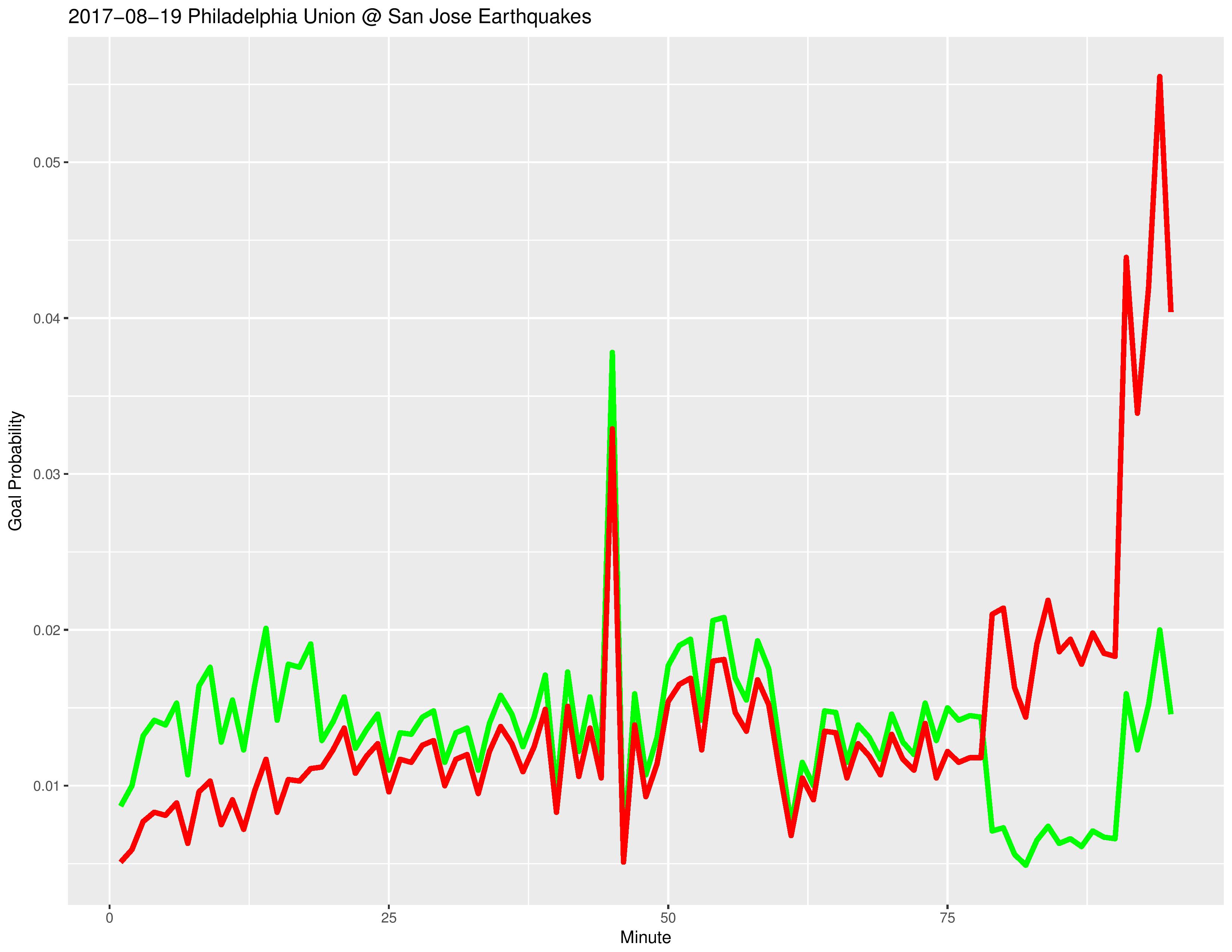
The following shows the changing raw probability of the two teams each scoring a goal. Green is Philadelphia’s probability of scoring a goal and red is their opponent’s probability of scoring a goal.
The reason for the spike at the 45th minute is because ’45+x’ is condensed to the 45th minute (therefore increasing the frequency of goals occurring in the 45th minute) to avoid duplication with the actual 46th/47th/etc minute, whereas the same situation does not occur for ’90+x’ minute, for which we actually calculate the addition and attribute the action to the goals to the 91st/92nd/etc minute if they occur.
Philadelphia +/- Player Analysis
The ‘+’ is a measure counting how many goals were scored by the Union while the player was on the field. The ‘-‘ counts how many goals were scored against the Union while the player was on the field.
| Player | Net | + | – | MINS | Net/90 | +/90 | -/90 | |
|---|---|---|---|---|---|---|---|---|
| 1 | Chris Pontius | 8 | 26 | 18 | 3521 | 0.204 | 0.665 | 0.460 |
| 2 | Oguchi Onyewu | 8 | 28 | 20 | 4320 | 0.167 | 0.583 | 0.417 |
| 3 | Jack Elliott | 7 | 29 | 22 | 4484 | 0.140 | 0.582 | 0.442 |
| 4 | Raymon Gaddis | 6 | 28 | 22 | 4386 | 0.123 | 0.575 | 0.451 |
| 5 | Andre Blake | 4 | 24 | 20 | 3960 | 0.091 | 0.545 | 0.455 |
| 6 | Derrick Jones | 3 | 12 | 9 | 1523 | 0.177 | 0.709 | 0.532 |
| 7 | Giliano Wijnaldum | 3 | 16 | 13 | 2547 | 0.106 | 0.565 | 0.459 |
| 8 | Ilsinho | 3 | 21 | 18 | 2732 | 0.099 | 0.692 | 0.593 |
| 9 | CJ Sapong | 3 | 33 | 30 | 5524 | 0.049 | 0.538 | 0.489 |
| 10 | Warren Creavalle | 2 | 4 | 2 | 334 | 0.539 | 1.078 | 0.539 |
| 11 | Alejandro Bedoya | 2 | 28 | 26 | 4860 | 0.037 | 0.519 | 0.481 |
| 12 | Haris Medunjanin | 1 | 34 | 33 | 6021 | 0.015 | 0.508 | 0.493 |
| 13 | Fabian Herbers | 0 | 8 | 8 | 660 | 0.000 | 1.091 | 1.091 |
| 14 | Fabinho | -1 | 18 | 19 | 3330 | -0.027 | 0.486 | 0.514 |
| 15 | Fafa Picault | -1 | 18 | 19 | 2874 | -0.031 | 0.564 | 0.595 |
| 16 | Marcus Epps | -2 | 5 | 7 | 554 | -0.325 | 0.812 | 1.137 |
| 17 | Adam Najem | -2 | 1 | 3 | 142 | -1.268 | 0.634 | 1.901 |
| 18 | John McCarthy | -3 | 10 | 13 | 2070 | -0.130 | 0.435 | 0.565 |
| 19 | Roland Alberg | -4 | 10 | 14 | 1351 | -0.266 | 0.666 | 0.933 |
| 20 | Joshua Yaro | -5 | 3 | 8 | 786 | -0.573 | 0.344 | 0.916 |
| 21 | Jay Simpson | -5 | 4 | 9 | 350 | -1.286 | 1.029 | 2.314 |
| 22 | Keegan Rosenberry | -6 | 6 | 12 | 1483 | -0.364 | 0.364 | 0.728 |
| 23 | Richie Marquez | -8 | 8 | 16 | 1953 | -0.369 | 0.369 | 0.737 |
| HomeAway | Player | Net | + | – | MINS | Net/90 | +/90 | -/90 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Home | Andre Blake | 10 | 17 | 7 | 2160 | 0.417 | 0.708 | 0.292 |
| 2 | Home | Chris Pontius | 9 | 19 | 10 | 2336 | 0.347 | 0.732 | 0.385 |
| 3 | Home | Alejandro Bedoya | 9 | 20 | 11 | 2790 | 0.290 | 0.645 | 0.355 |
| 4 | Home | Oguchi Onyewu | 9 | 20 | 11 | 2790 | 0.290 | 0.645 | 0.355 |
| 5 | Home | CJ Sapong | 9 | 22 | 13 | 3121 | 0.260 | 0.634 | 0.375 |
| 6 | Home | Ilsinho | 7 | 17 | 10 | 1886 | 0.334 | 0.811 | 0.477 |
| 7 | Home | Raymon Gaddis | 7 | 19 | 12 | 2678 | 0.235 | 0.639 | 0.403 |
| 8 | Home | Jack Elliott | 7 | 19 | 12 | 2734 | 0.230 | 0.625 | 0.395 |
| 9 | Home | Haris Medunjanin | 7 | 23 | 16 | 3501 | 0.180 | 0.591 | 0.411 |
| 10 | Home | Derrick Jones | 4 | 9 | 5 | 1018 | 0.354 | 0.796 | 0.442 |
| 11 | Home | Fabinho | 4 | 11 | 7 | 1620 | 0.222 | 0.611 | 0.389 |
| 12 | Home | Giliano Wijnaldum | 4 | 12 | 8 | 1769 | 0.204 | 0.611 | 0.407 |
| 13 | Home | Fabian Herbers | 3 | 4 | 1 | 241 | 1.120 | 1.494 | 0.373 |
| 14 | Home | Marcus Epps | 1 | 4 | 3 | 430 | 0.209 | 0.837 | 0.628 |
| 15 | Home | Fafa Picault | 0 | 10 | 10 | 1558 | 0.000 | 0.578 | 0.578 |
| 16 | Home | Richie Marquez | 0 | 6 | 6 | 912 | 0.000 | 0.592 | 0.592 |
| 17 | Home | Roland Alberg | 0 | 6 | 6 | 747 | 0.000 | 0.723 | 0.723 |
| 18 | Home | Keegan Rosenberry | -1 | 4 | 5 | 673 | -0.134 | 0.535 | 0.669 |
| 19 | Home | Adam Najem | -1 | 1 | 2 | 123 | -0.732 | 0.732 | 1.463 |
| 20 | Home | Jay Simpson | -2 | 3 | 5 | 305 | -0.590 | 0.885 | 1.475 |
| 21 | Home | Warren Creavalle | -2 | 0 | 2 | 158 | -1.139 | 0.000 | 1.139 |
| 22 | Home | John McCarthy | -3 | 6 | 9 | 1350 | -0.200 | 0.400 | 0.600 |
| 23 | Home | Joshua Yaro | -4 | 1 | 5 | 336 | -1.071 | 0.268 | 1.339 |
| HomeAway | Player | Net | + | – | MINS | Net/90 | +/90 | -/90 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Away | Warren Creavalle | 4 | 4 | 0 | 176 | 2.045 | 2.045 | 0.000 |
| 2 | Away | Jack Elliott | 0 | 10 | 10 | 1750 | 0.000 | 0.514 | 0.514 |
| 3 | Away | John McCarthy | 0 | 4 | 4 | 720 | 0.000 | 0.500 | 0.500 |
| 4 | Away | Raymon Gaddis | -1 | 9 | 10 | 1708 | -0.053 | 0.474 | 0.527 |
| 5 | Away | Oguchi Onyewu | -1 | 8 | 9 | 1530 | -0.059 | 0.471 | 0.529 |
| 6 | Away | Fafa Picault | -1 | 8 | 9 | 1316 | -0.068 | 0.547 | 0.616 |
| 7 | Away | Chris Pontius | -1 | 7 | 8 | 1185 | -0.076 | 0.532 | 0.608 |
| 8 | Away | Giliano Wijnaldum | -1 | 4 | 5 | 778 | -0.116 | 0.463 | 0.578 |
| 9 | Away | Derrick Jones | -1 | 3 | 4 | 505 | -0.178 | 0.535 | 0.713 |
| 10 | Away | Joshua Yaro | -1 | 2 | 3 | 450 | -0.200 | 0.400 | 0.600 |
| 11 | Away | Adam Najem | -1 | 0 | 1 | 19 | -4.737 | 0.000 | 4.737 |
| 12 | Away | Fabian Herbers | -3 | 4 | 7 | 419 | -0.644 | 0.859 | 1.504 |
| 13 | Away | Marcus Epps | -3 | 1 | 4 | 124 | -2.177 | 0.726 | 2.903 |
| 14 | Away | Jay Simpson | -3 | 1 | 4 | 45 | -6.000 | 2.000 | 8.000 |
| 15 | Away | Ilsinho | -4 | 4 | 8 | 846 | -0.426 | 0.426 | 0.851 |
| 16 | Away | Roland Alberg | -4 | 4 | 8 | 604 | -0.596 | 0.596 | 1.192 |
| 17 | Away | Fabinho | -5 | 7 | 12 | 1710 | -0.263 | 0.368 | 0.632 |
| 18 | Away | Keegan Rosenberry | -5 | 2 | 7 | 810 | -0.556 | 0.222 | 0.778 |
| 19 | Away | Haris Medunjanin | -6 | 11 | 17 | 2520 | -0.214 | 0.393 | 0.607 |
| 20 | Away | CJ Sapong | -6 | 11 | 17 | 2403 | -0.225 | 0.412 | 0.637 |
| 21 | Away | Andre Blake | -6 | 7 | 13 | 1800 | -0.300 | 0.350 | 0.650 |
| 22 | Away | Alejandro Bedoya | -7 | 8 | 15 | 2070 | -0.304 | 0.348 | 0.652 |
| 23 | Away | Richie Marquez | -8 | 2 | 10 | 1041 | -0.692 | 0.173 | 0.865 |
Model Validation
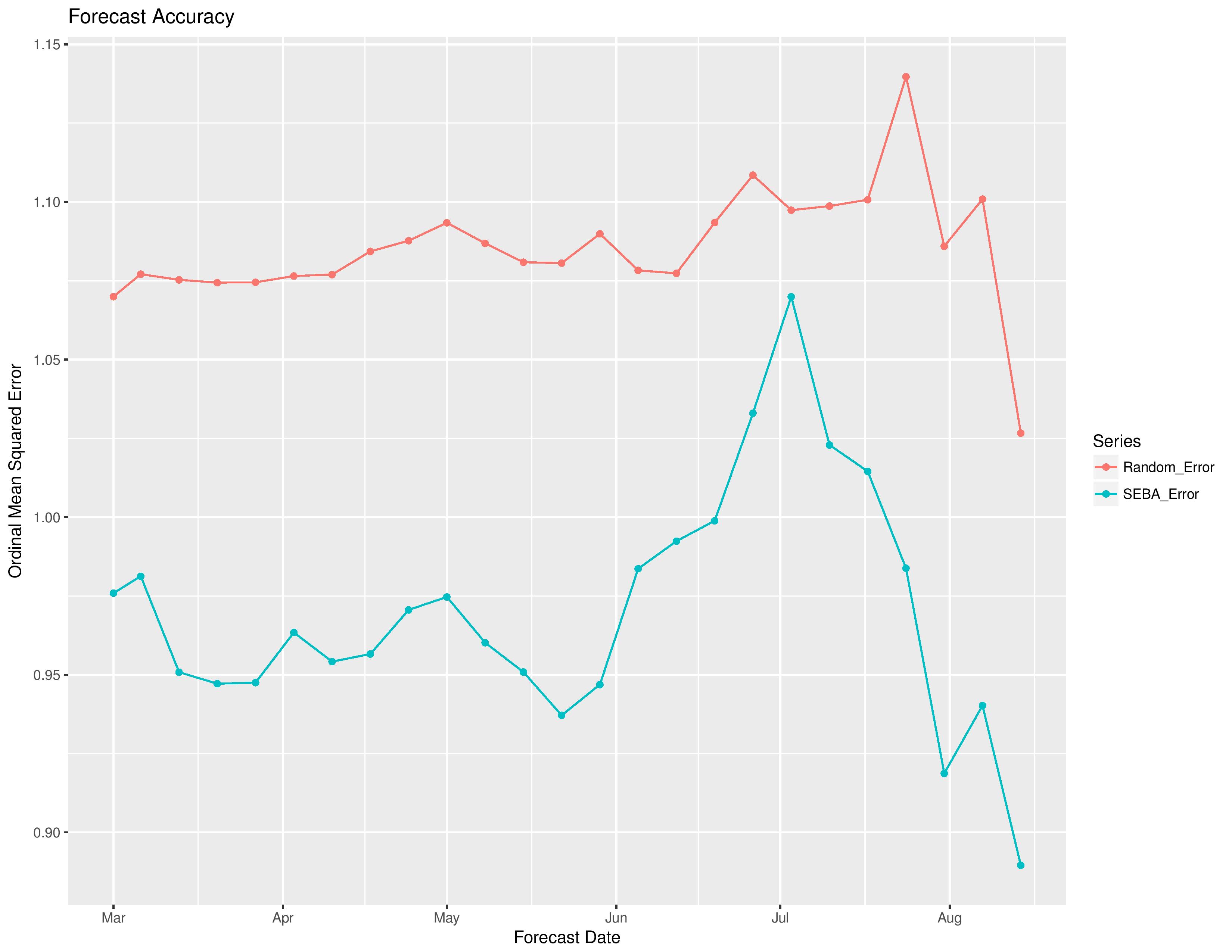
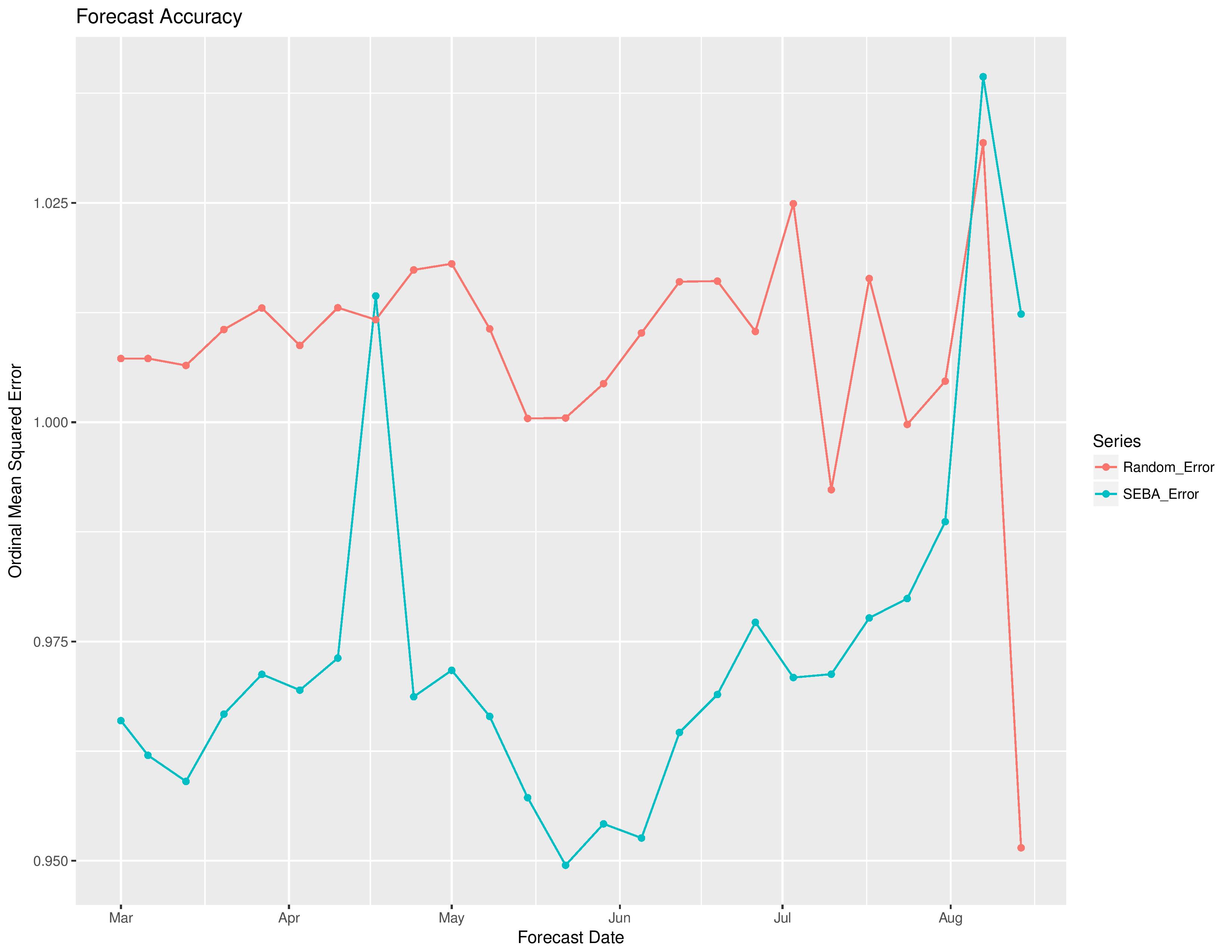
The following shows the degree of error by the model vs the error if the model was purely random without intelligence. The x-axis is based on the date from which the forecast was made (this will update throughout the season as more results are finalized and compared with predictions). The ordinal squared error metric (not a traditional metric) is calculated as:
(ProbW – ActW)^2 + (ProbT – ActT)^2 + (ProbL – ActL)^2 +
((ProbW + ProbT) – (ActW + ActT))^2 +
((ProbL + ProbT) – (ActL + ActT))^2
where Prob[W/T/L] is the model’s probability of resulting outcomes and Act[W/T/L] is a 1 or 0 representation of whether it actually happened.
Random errors will decline when more ties occur as there is a less severe penalty for ties.
We should expect random errors to remain relatively constant over time, where our model’s errors will hopefully decline as the season goes on as it gathers new information.
These data points are not fixed until the end of the season due to additional matches adding to them.
USL
Power Rankings
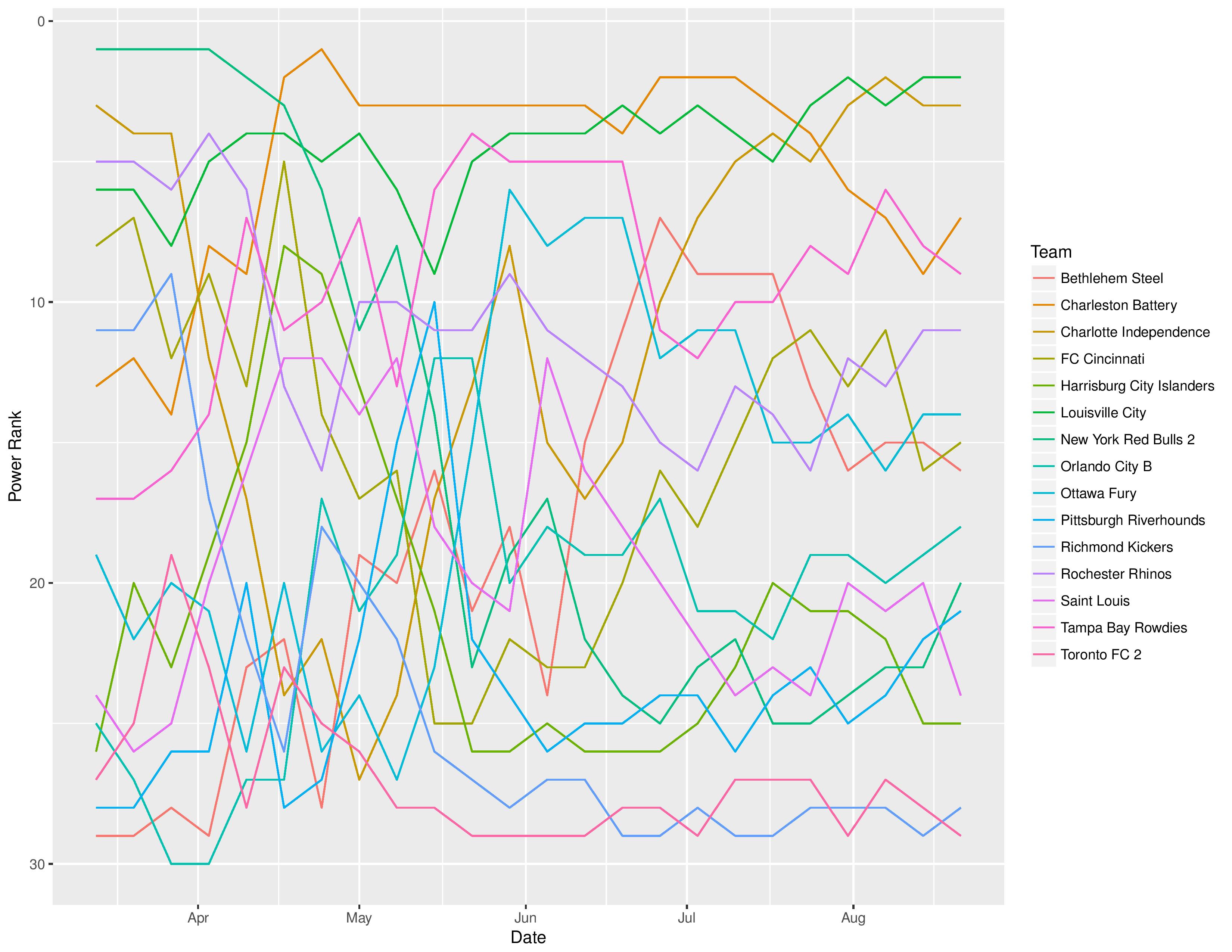
SEBA has the Bethlehem Steel decreasing from 15th to 16th while it has Harrisburg City remained at 25th.

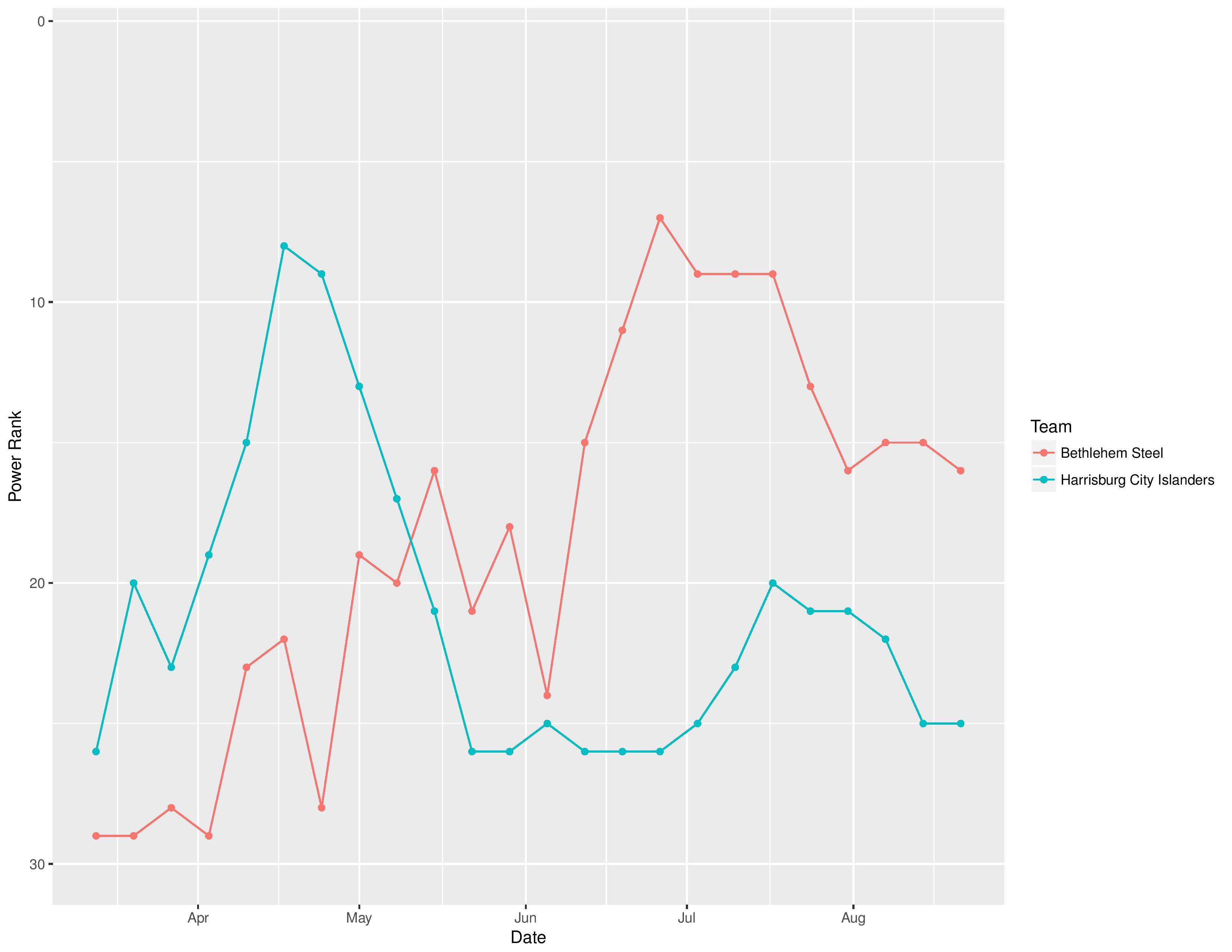
The following shows the evolution of SEBA’s power rankings for the USL East over time.
Playoffs probability and more
Bethlehem’s playoff odds have decreased from 88.4% to 72.0% while Harrisburg City’s odds of reaching the postseason have decreased from 1.6% to 1.5%.

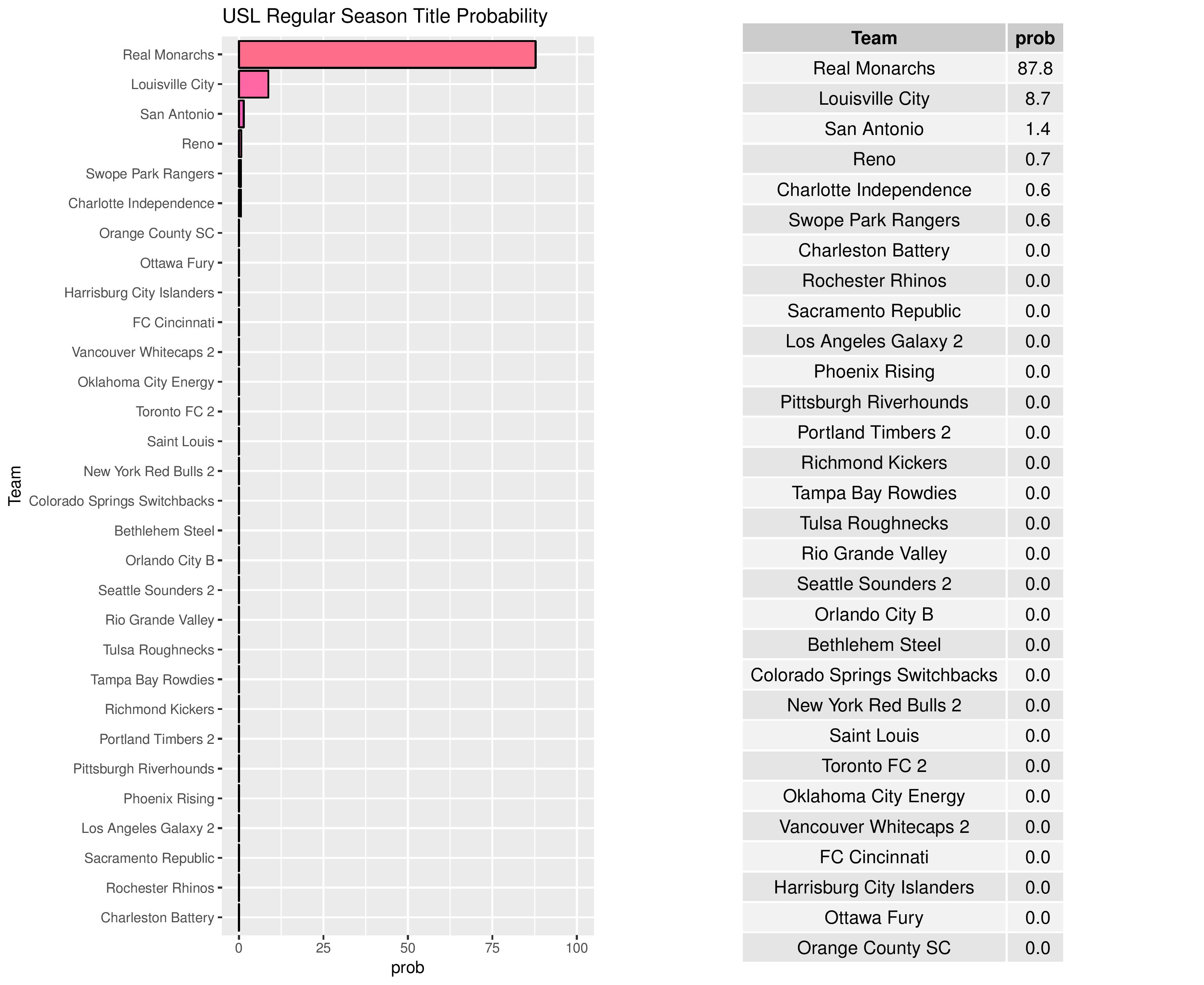
Bethlehem’s odds at becoming the USL Champion have decreased from 1.7% to 1.1% while Harrisburg City’s remained at practically zero:
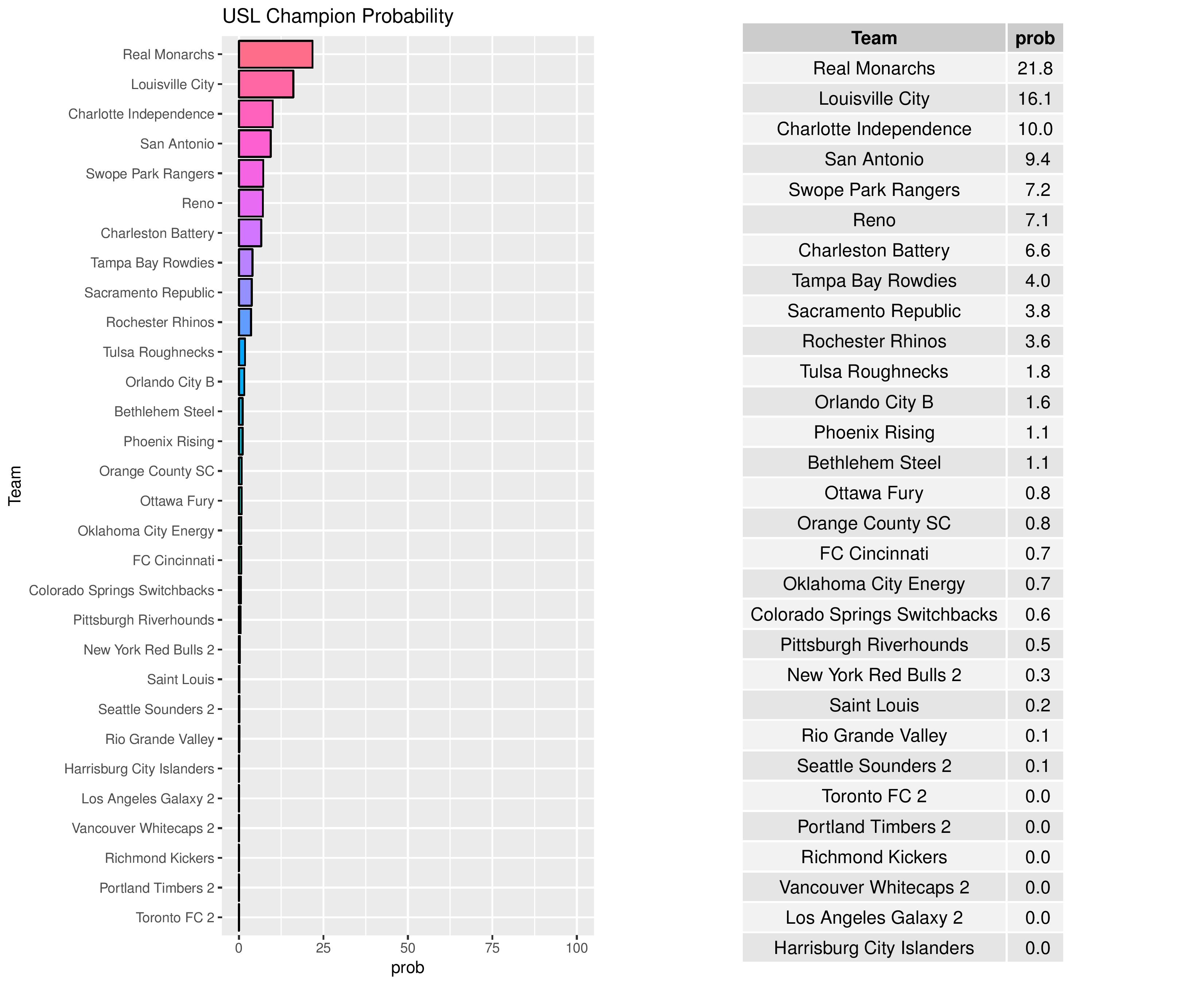
Over time, we can see how the odds for different prizes change for Bethlehem and Harrisburg.


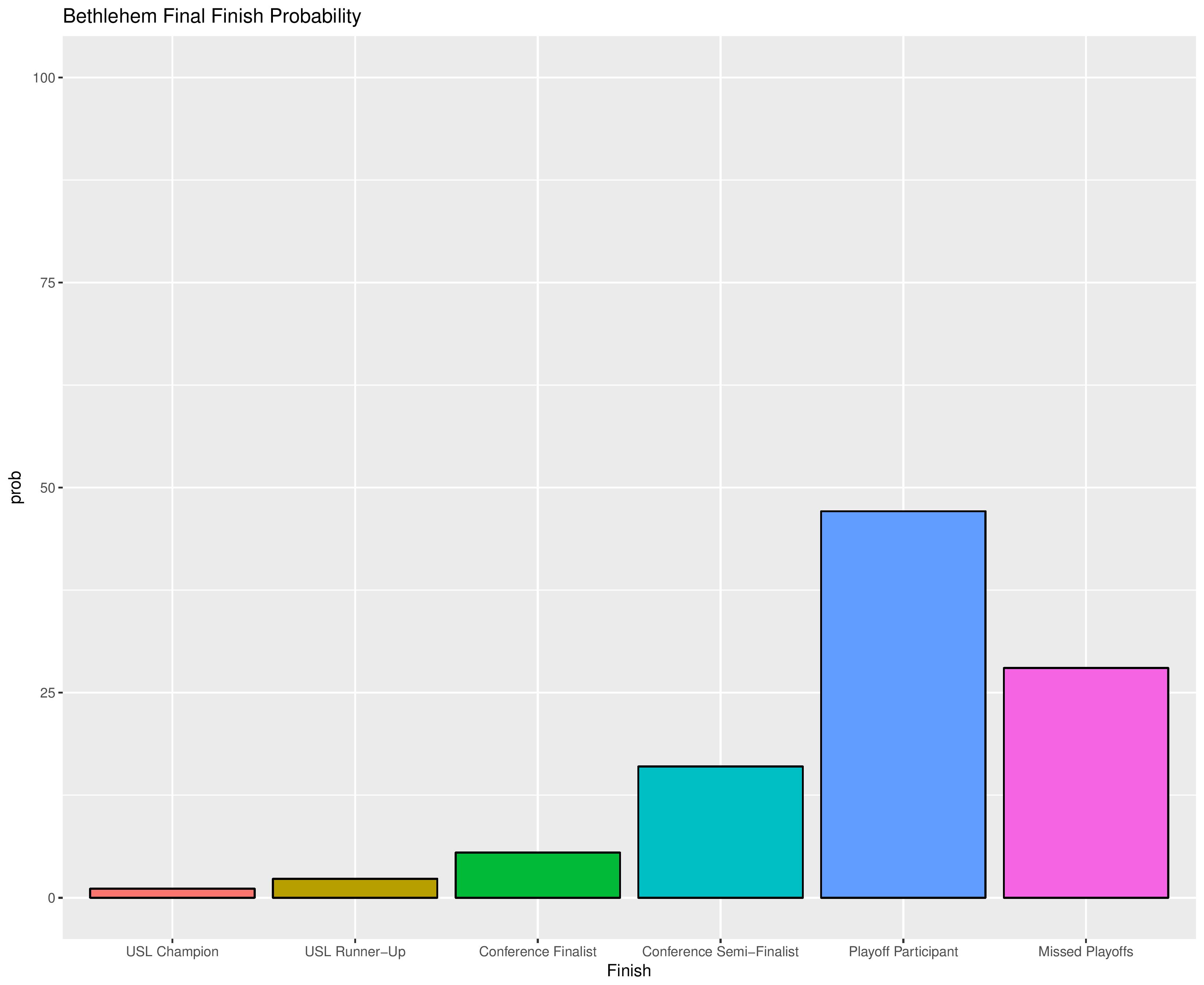
The following are probabilities for each category of outcomes for Bethlehem.
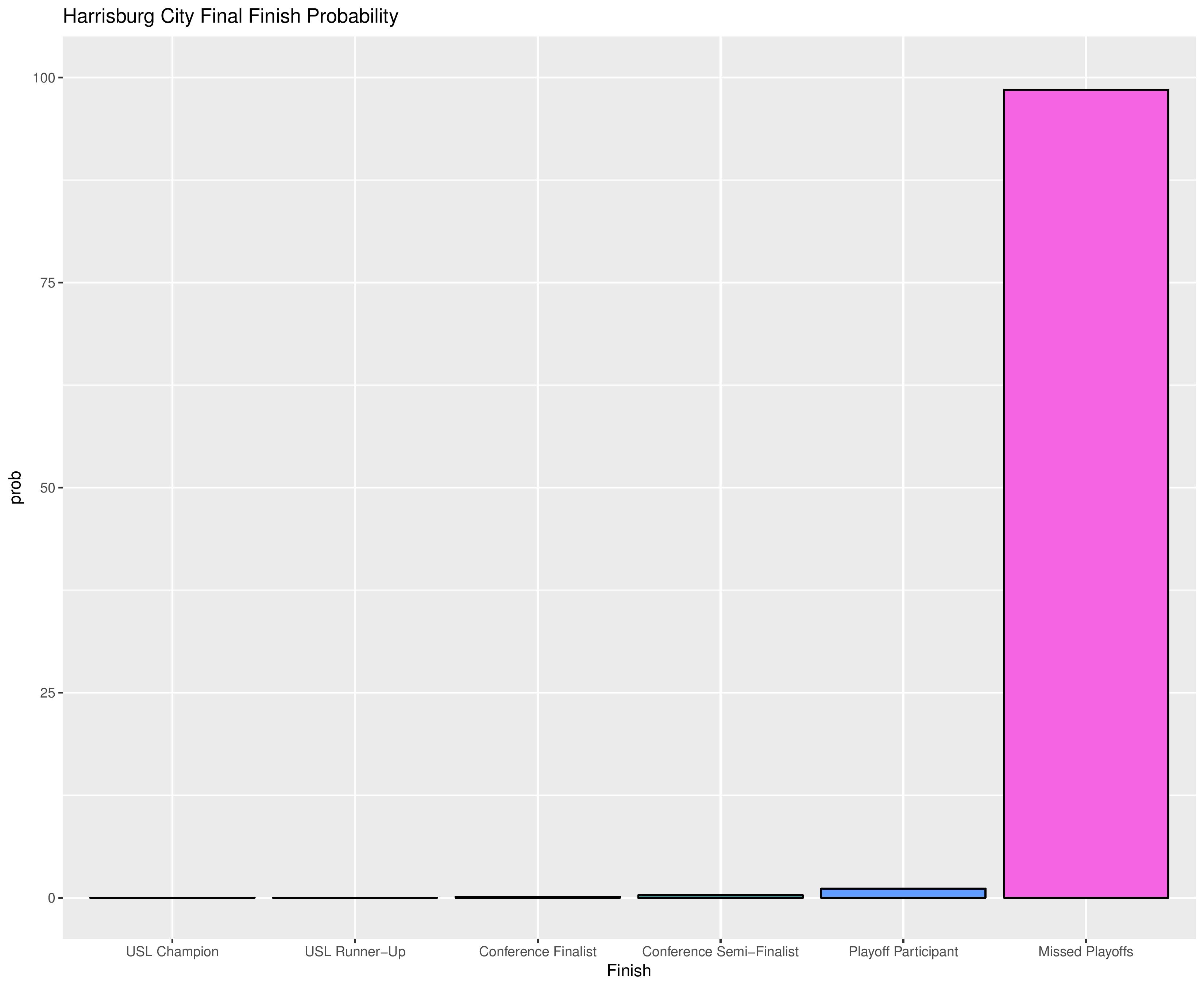
The following are probabilities for each category of outcomes for Harrisburg City:
The following shows the probability of each post-playoff ranking finish:
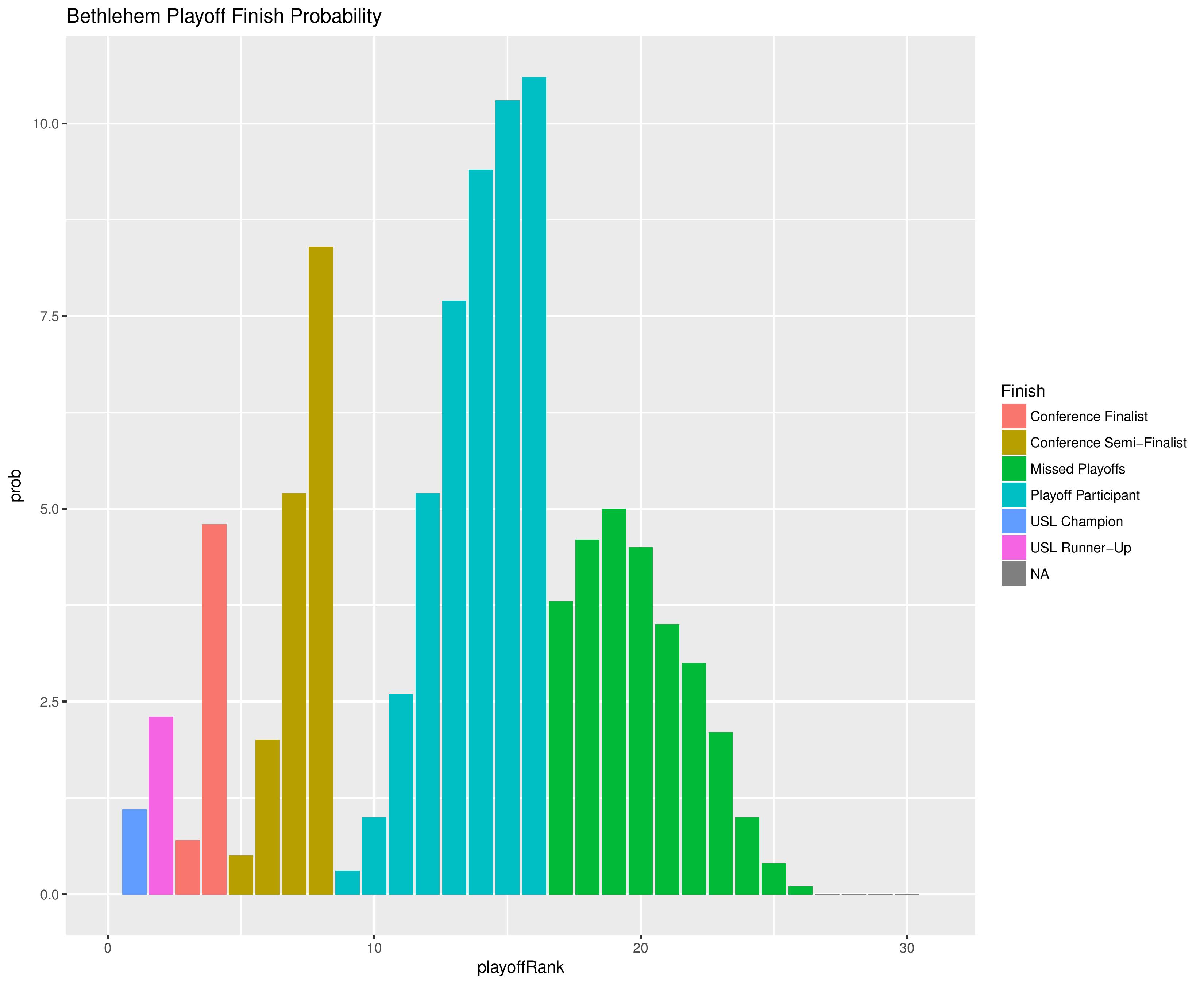
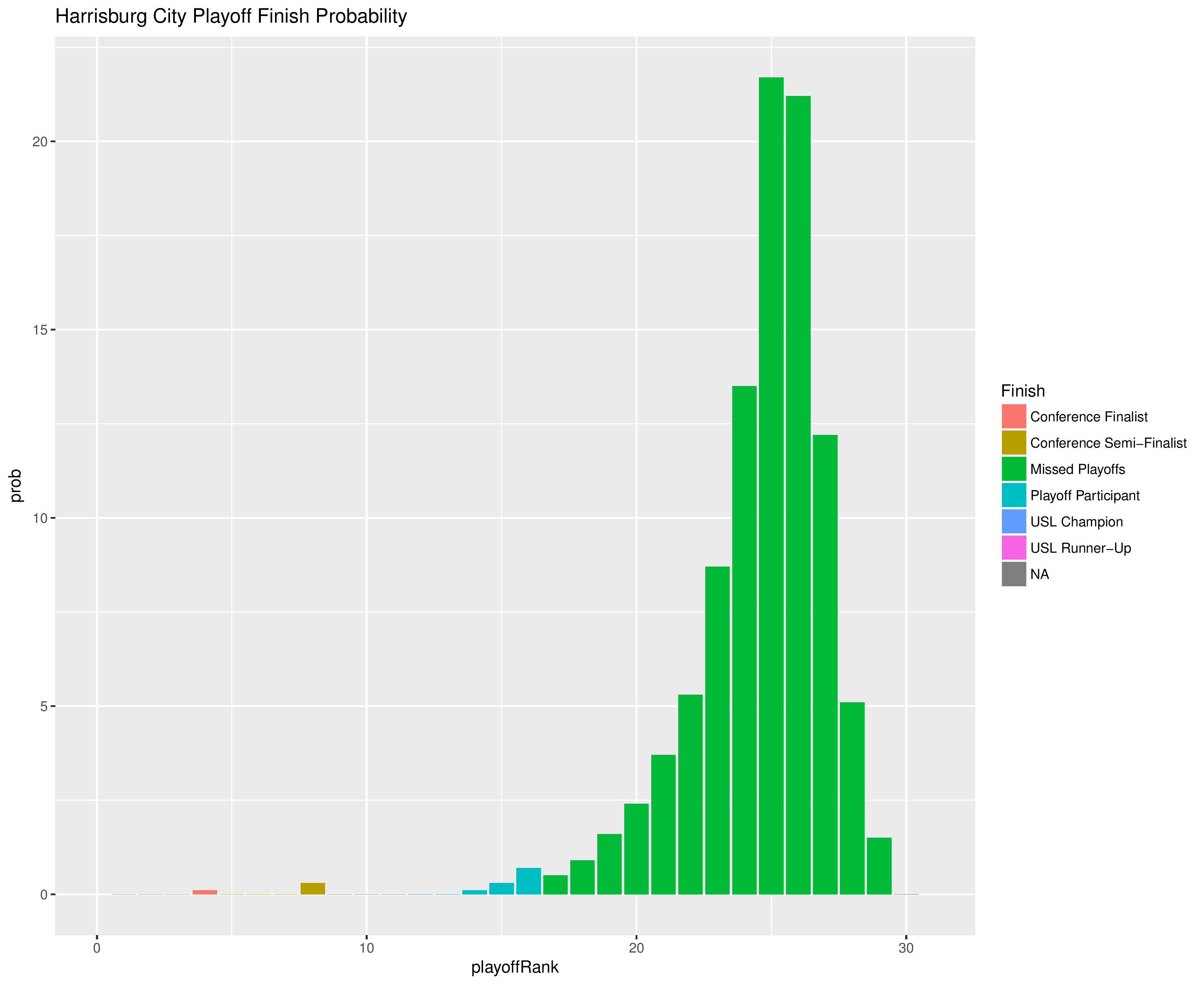
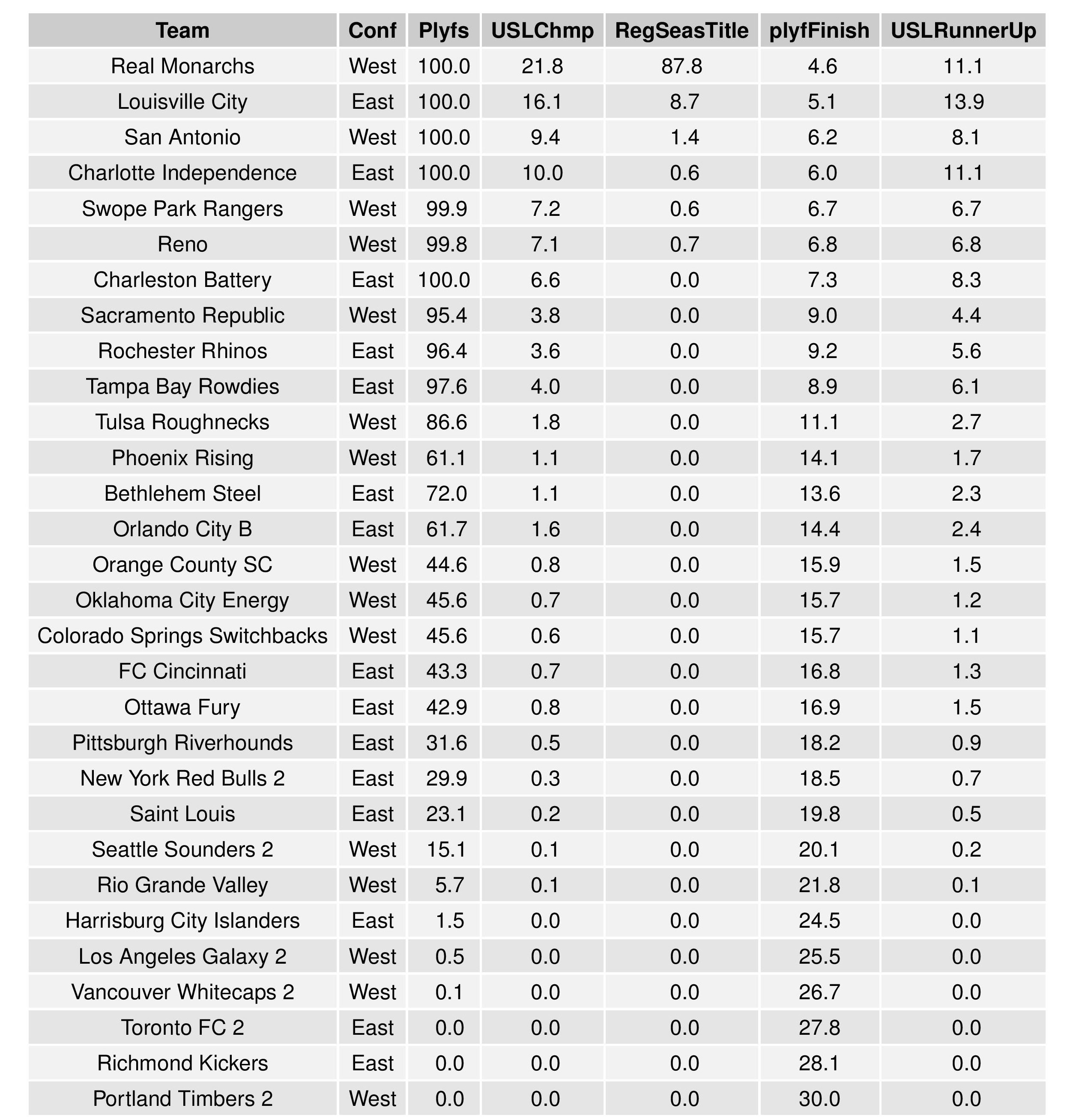
The following shows the summary of simulations in an easy table format.
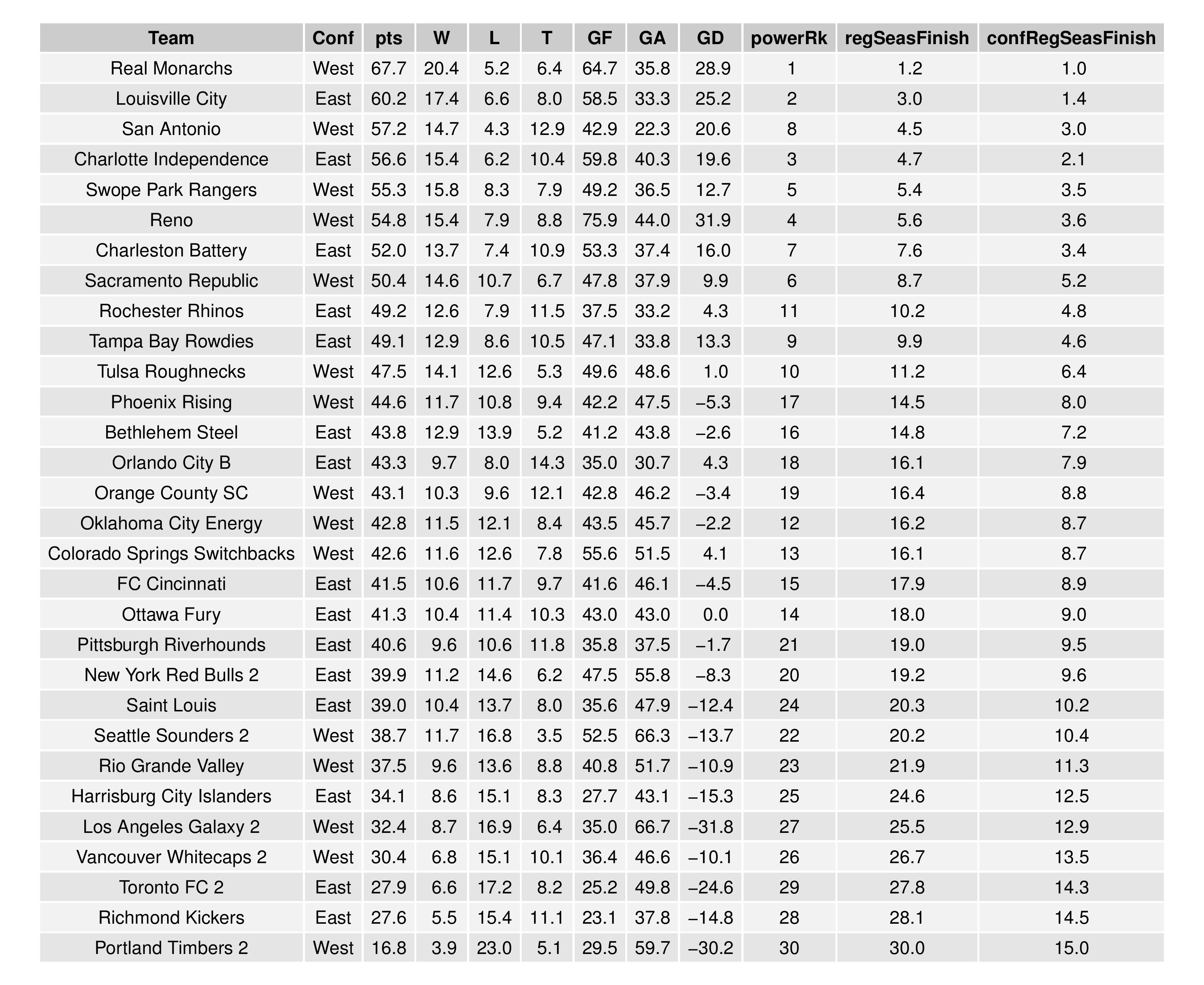
We can also show how the Remaining Strength of Schedule affects each team.
The “Points Percentage Advantage” shown on the X-axis represents the percentage of points expected over the league average schedule. This “points expected” value is generated by simulating how all teams would perform with all remaining schedules (and therefore judges a schedule based upon how all teams would perform in that scenario).
In short, the higher the value, the easier the remaining schedule.
Remaining home field advantage will make a large contribution here. It can also be true that a better team has an ‘easier’ schedule simply because they do not have to play themselves. Likewise, a bad team may have a ‘harder’ schedule because they also do not play themselves.
The table following the chart also shares helpful context with these percentages.
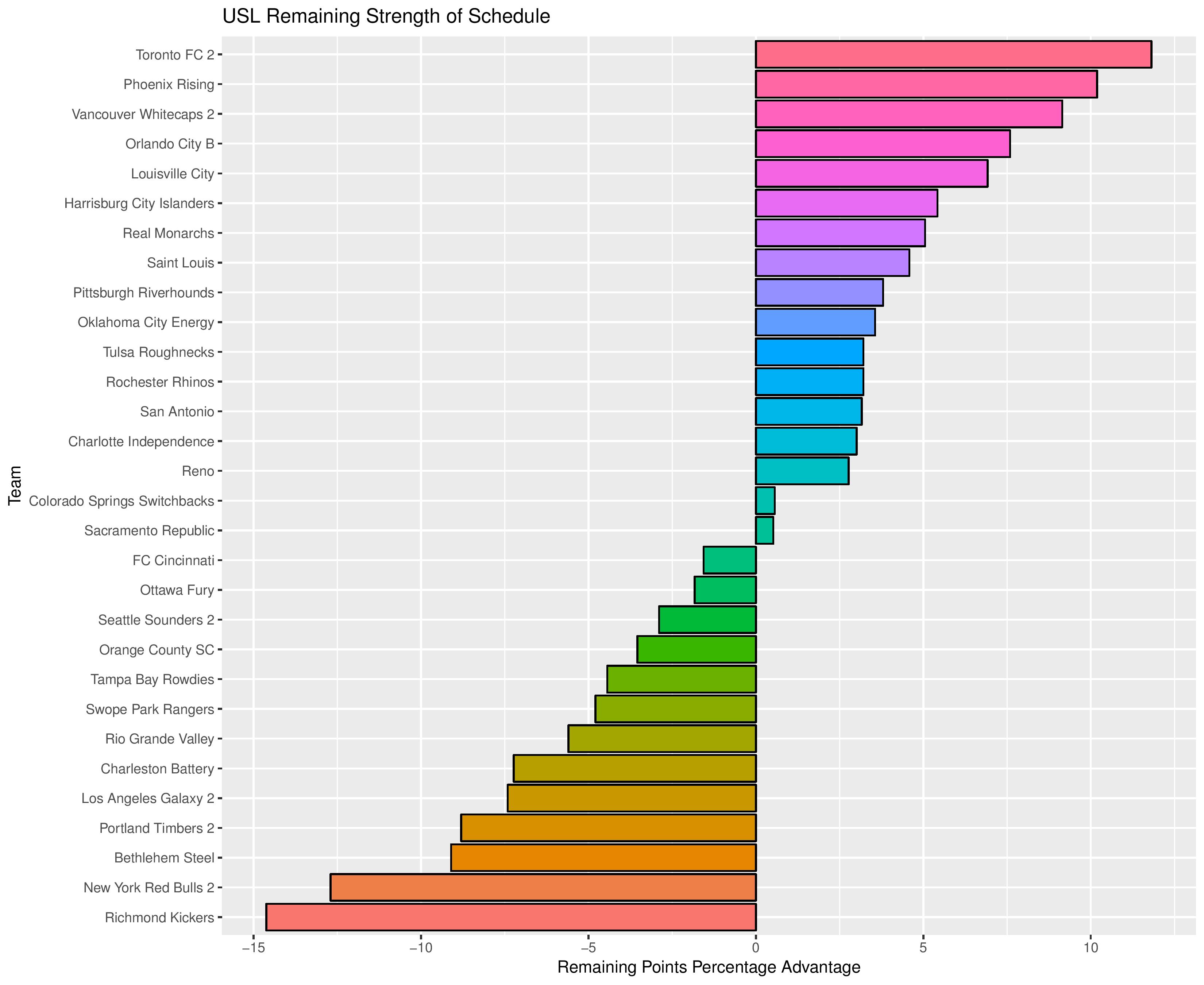
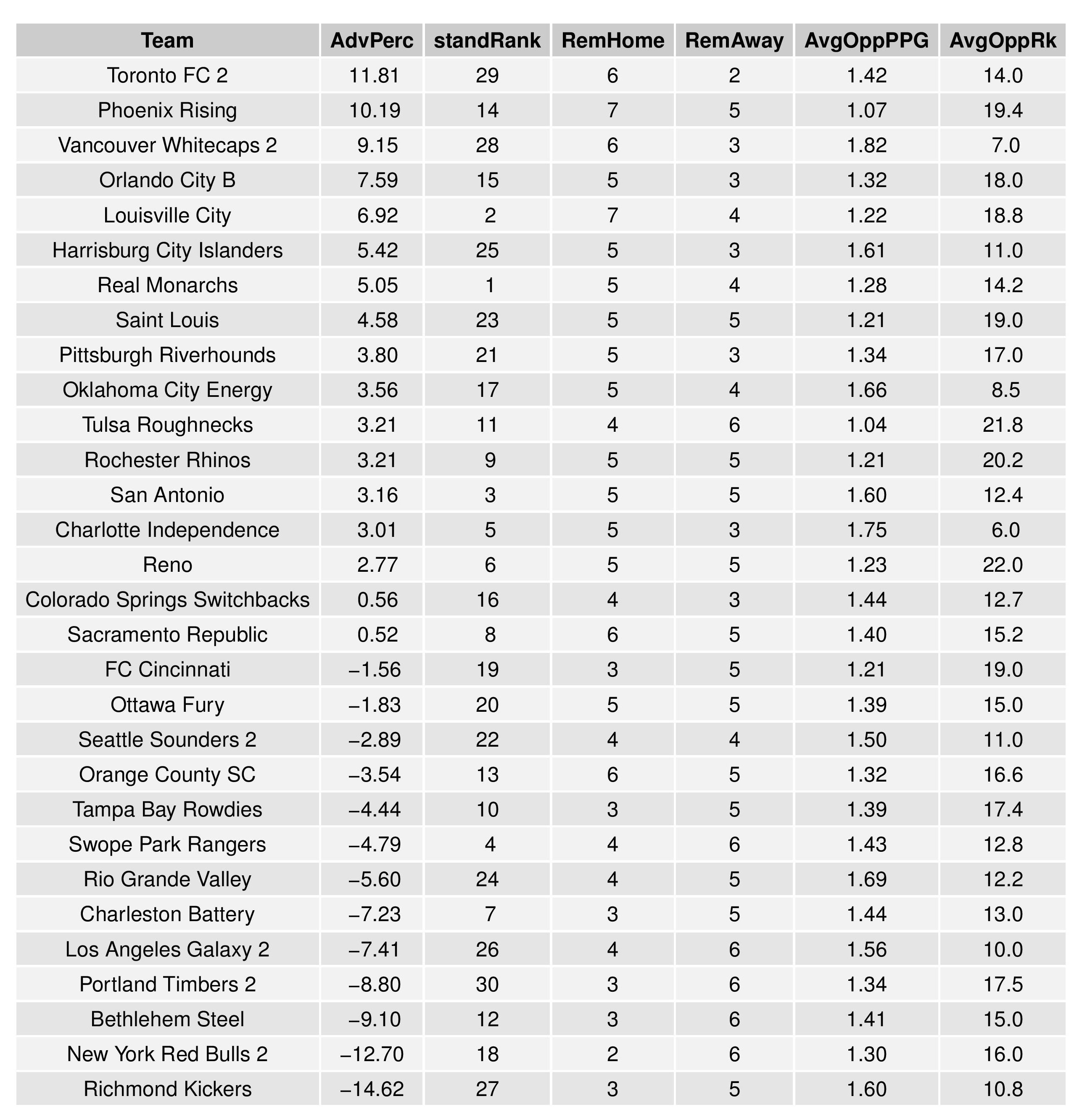
Accompanying the advantage percentage in the following table is their current standings rank (right now ties are not properly calculated beyond pts/gd/gf), the remaining home matches, the remaining away matches, the current average points-per-game of future opponents (results-based, not model-based), and the average power ranking of future opponents according to SEBA.
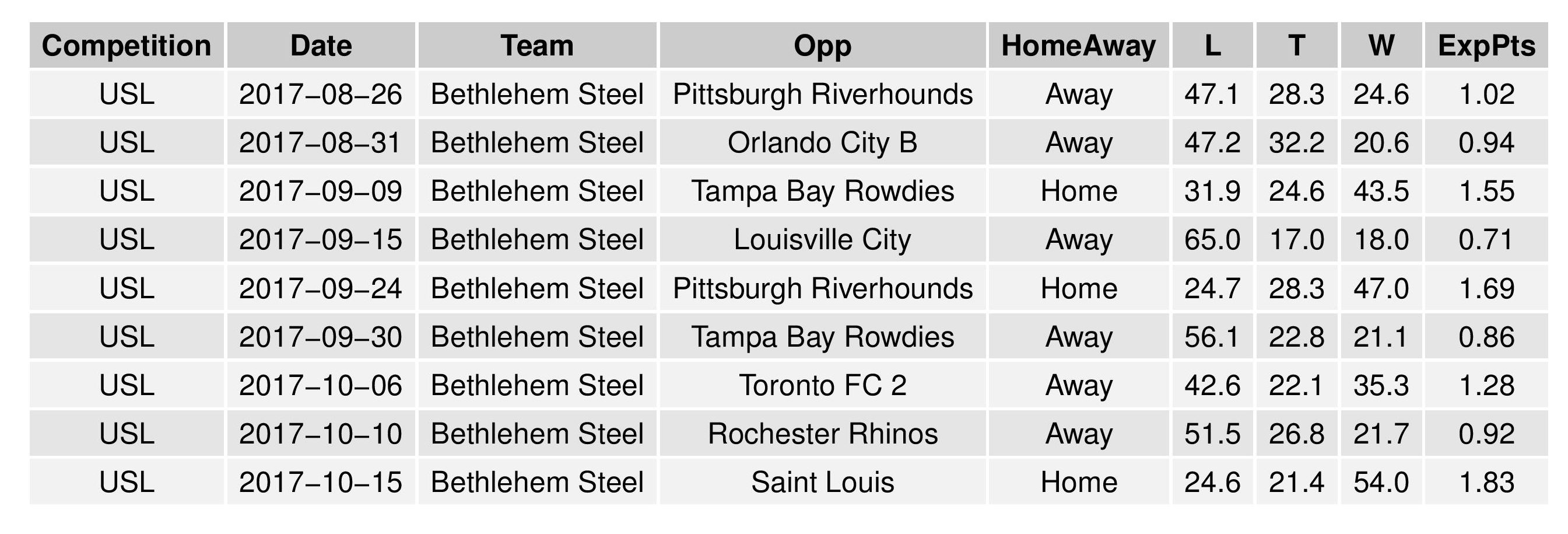
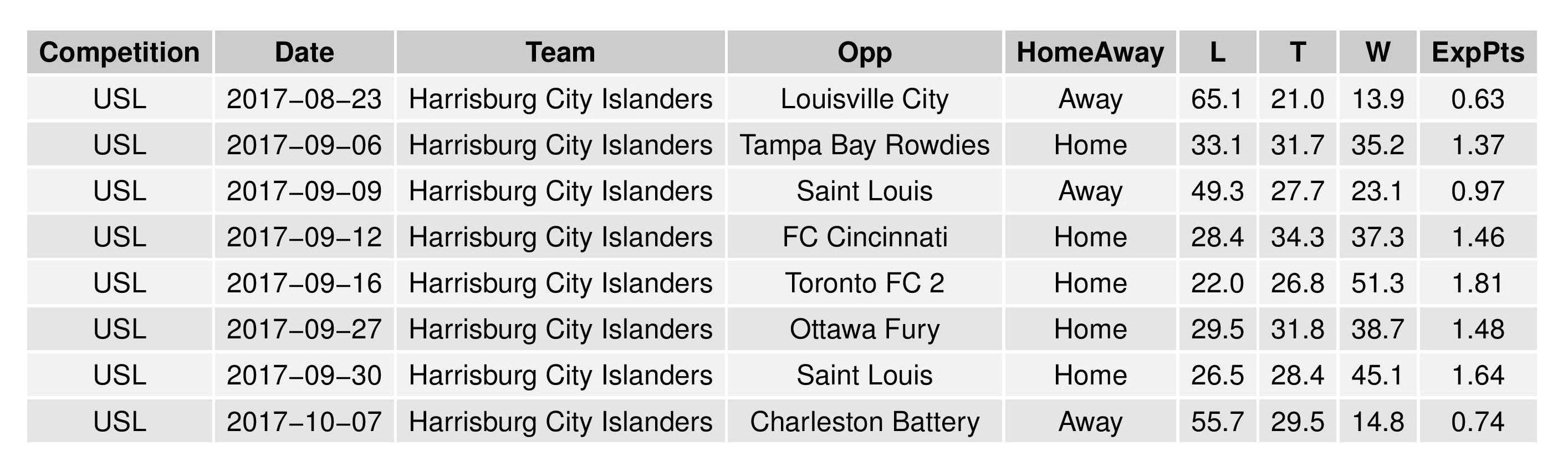
The following shows the expectations for upcoming matches for both Bethlehem and Harrisburg:
Model Validation
This chart is the same as that in the MLS forecast (except for USL matches instead of MLS).
Remember that these data points are not fixed until the end of the season.
NWSL
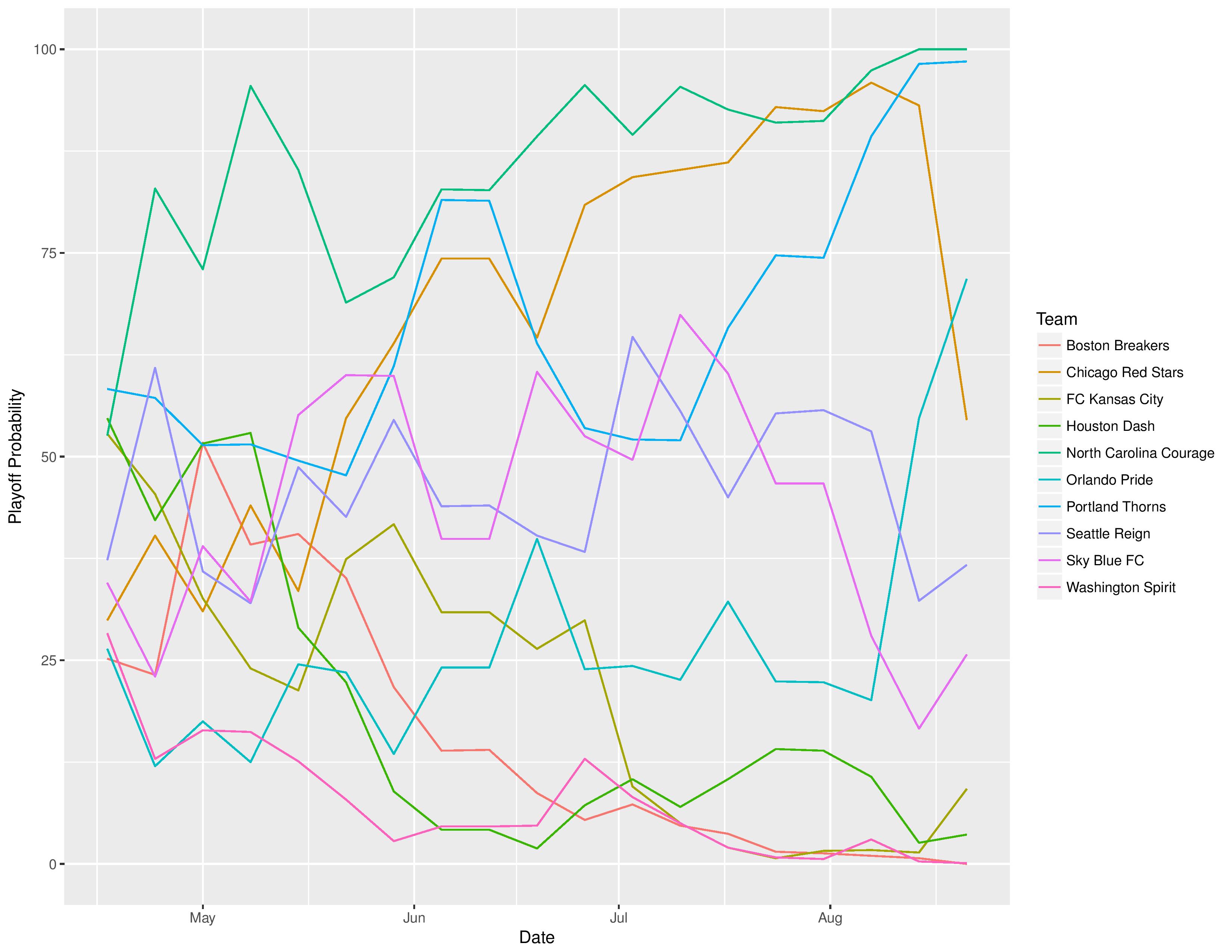
Power Rankings
Playoffs probability and more
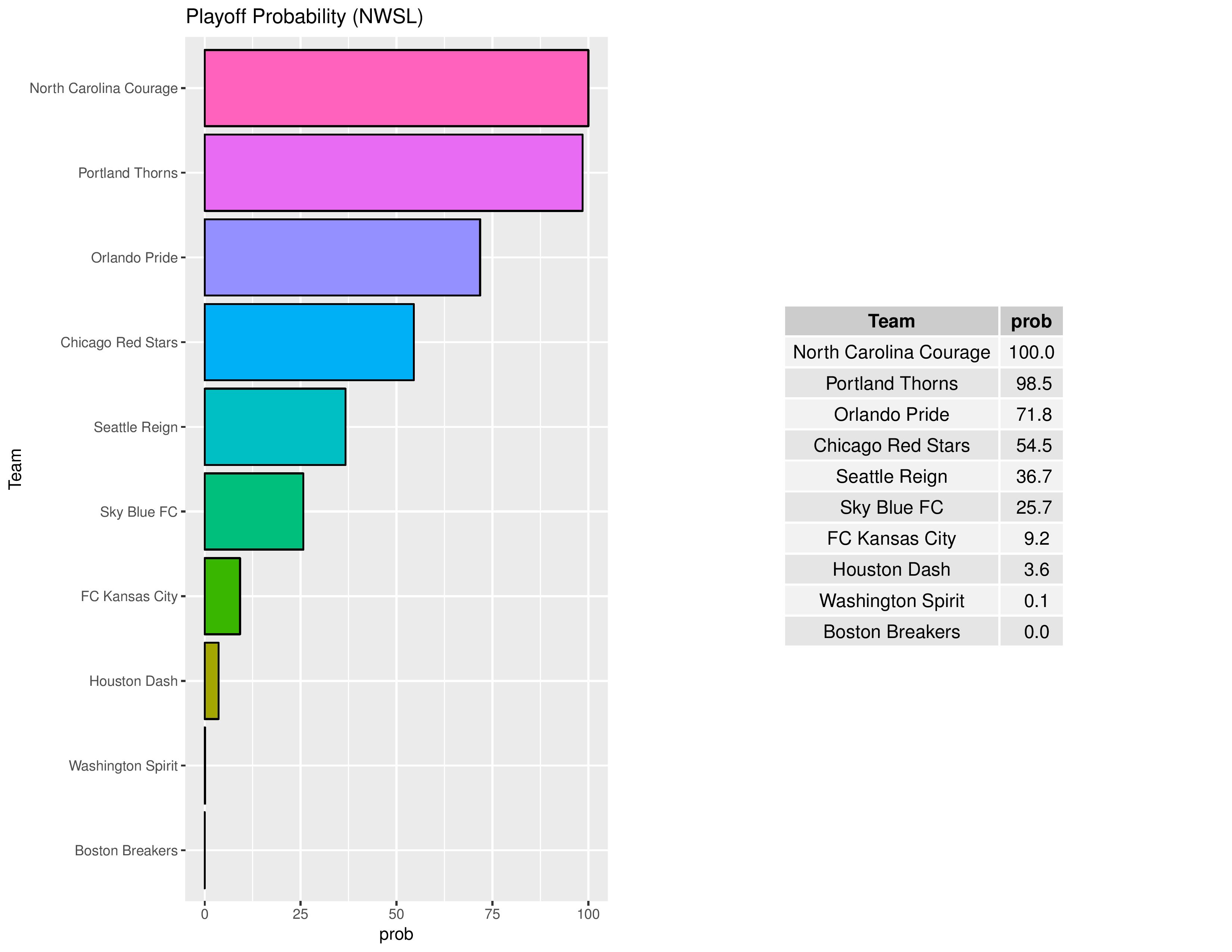
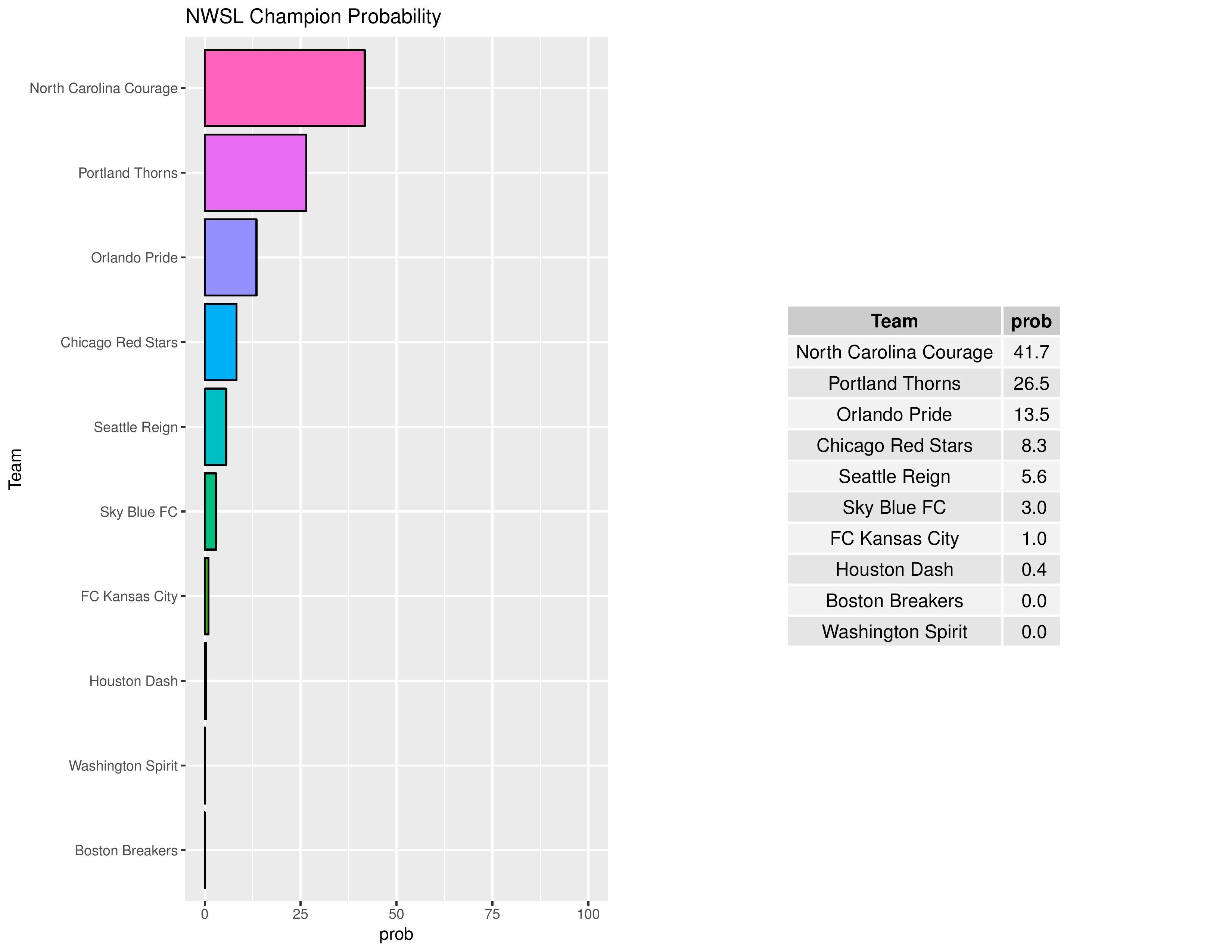

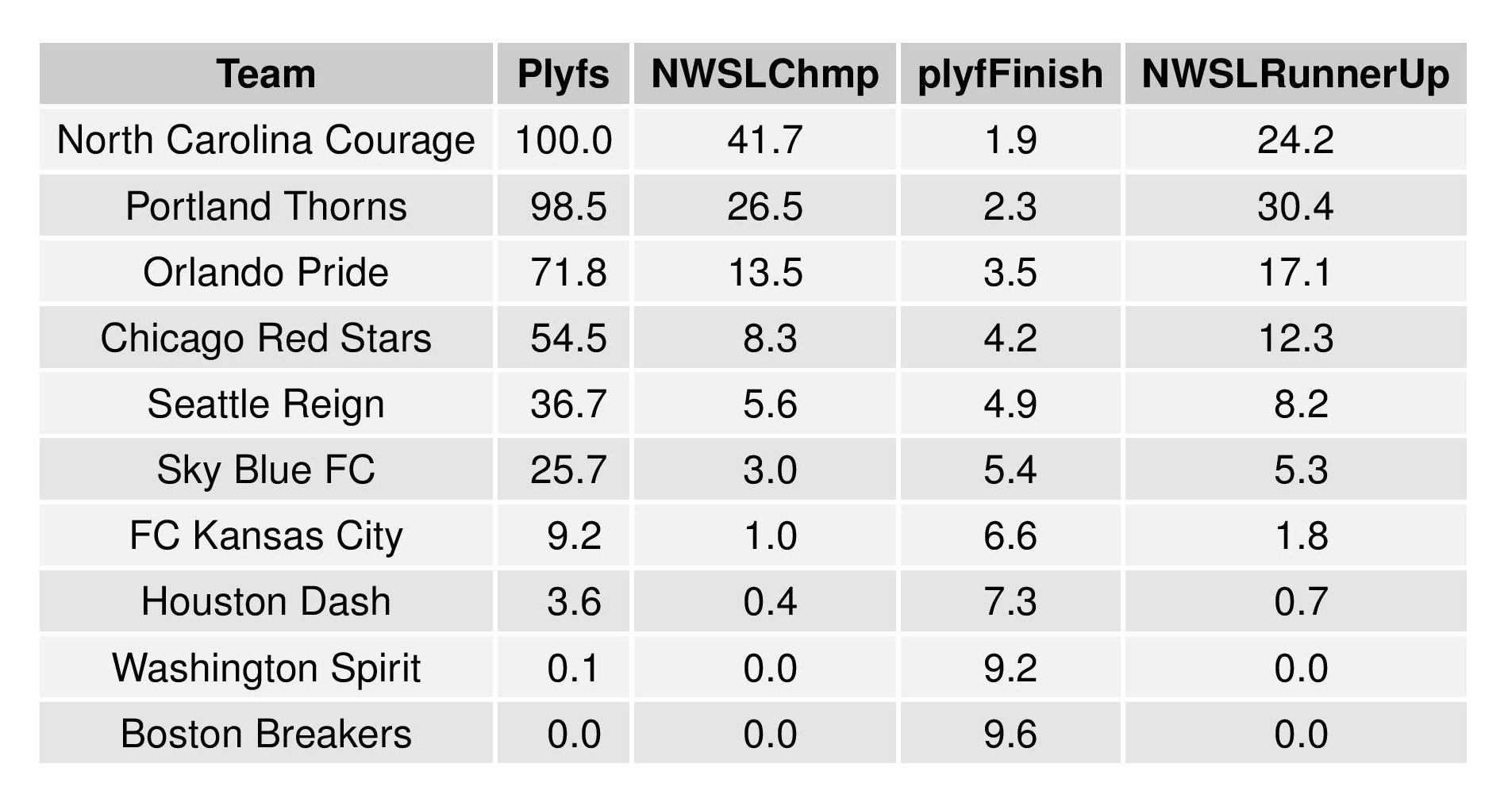
The following shows the summary of the simulations in an easy table format.

As a new feature, we can also show how the Remaining Strength of Schedule affects each team.
The “Points Percentage Advantage” shown on the X-axis represents the percentage of points expected over the league average schedule. This “points expected” value is generated by simulating how all teams would perform with all remaining schedules (and therefore judges a schedule based upon how all teams would perform in that scenario).
In short, the higher the value, the easier the remaining schedule.
It can also be true that a better team has an ‘easier’ schedule simply because they do not have to play themselves. Likewise, a bad team may have a ‘harder’ schedule because they also do not play themselves.
The table following the chart also shares helpful context with these percentages:
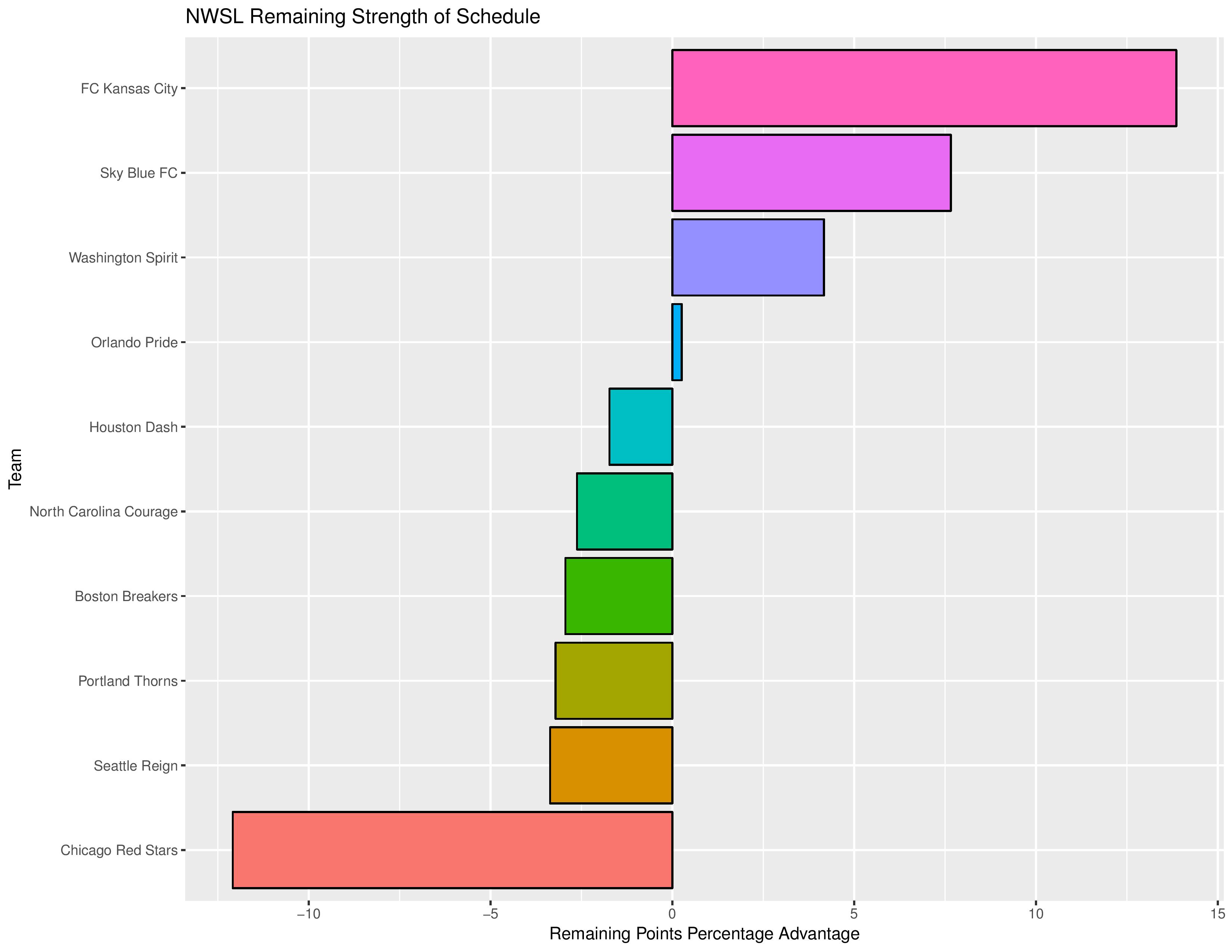
Accompanying the advantage percentage in the following table is their current standings rank (right now ties are not properly calculated beyond pts/gd/gf), the remaining home matches, the remaining away matches, the current average points-per-game of future opponents (results-based, not model-based), and the average power ranking of future opponents according to SEBA.
The SEBA Projection System is an acronym for a tortured collection of words in the Statistical Extrapolation Bayesian Analyzer Projection System. Check out the first season’s post to find out how it works (https://phillysoccerpage.net/2017/03/03/2017-initial-seba-projections/)

Love the “plus-minus” ratings for Union players!
.
Honesty compels that I state I have no idea how you get to the conclusions, but the conclusions are interesting, quite.
.
And I extract a detail that is no surprise, namely, Harris Medunjanin leads the team in minutes played.
.
I rely on your USL strength of schedule analysis, Chris. And I think carefully about your expectations for future matches for the Steel.
Thanks!
–
Out of curiosity, which conclusions do you mean? Are you talking about examples like the playoffs odds and remaining strength of schedule?